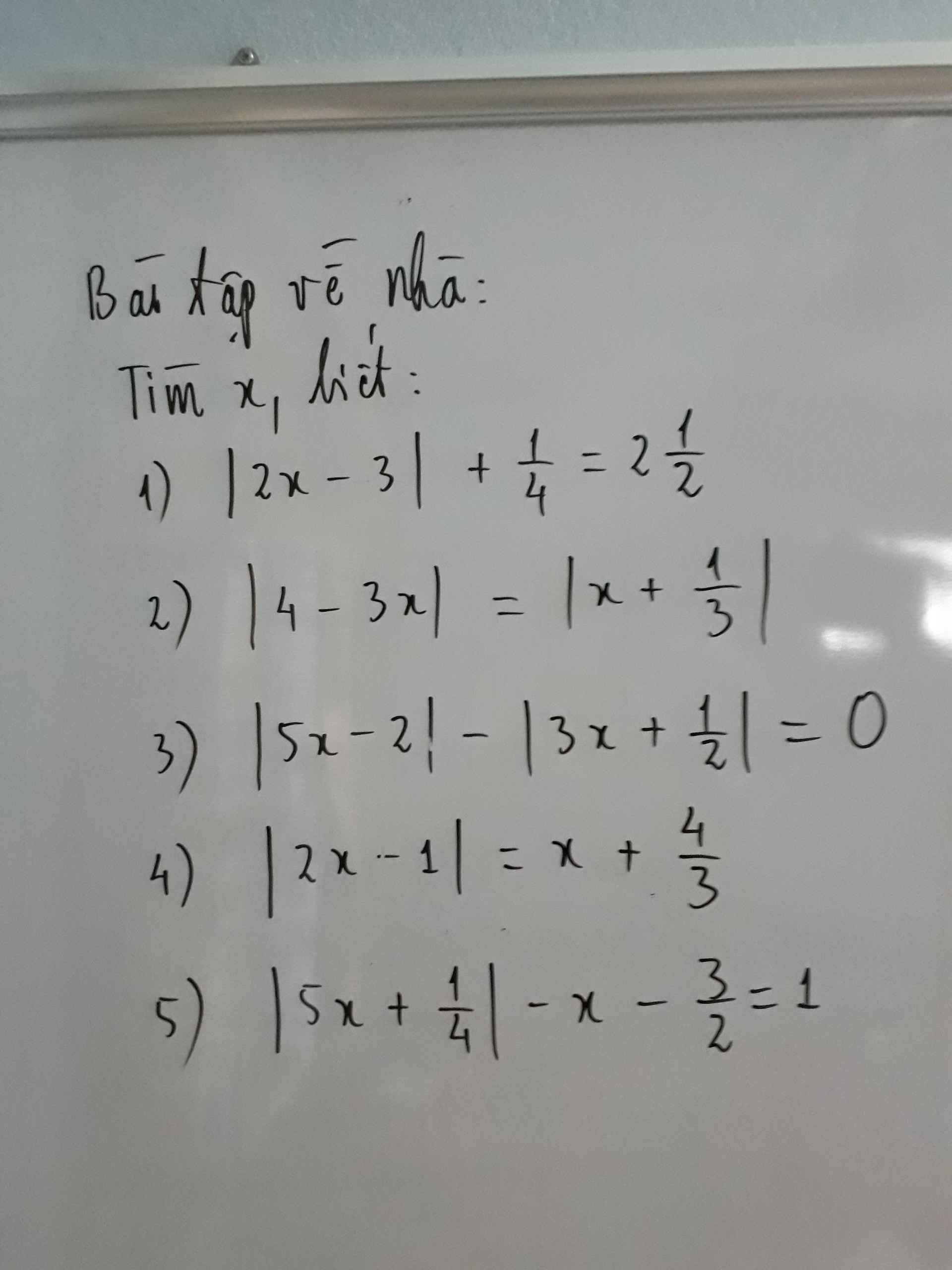Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)

1: Xét ΔMDB vuông tại D và ΔNEC vuông tại E có
BD=CE
góc MBD=góc NCE
=>ΔMDB=ΔNEC
=>DM=EN
2: DM//EN
DM=EN
=>DMEN là hình bình hành
=>I là trung điểm của MN



Câu 6
a) Ta có: \(\widehat{A}=90^0\) ⇒a⊥c
a//b, a⊥c ⇒b⊥c
b) Ta lại có: M1+N1=1800(trong cùng phía)
1200+N1=1800
N1=1800-1200=600


0,25 : x = x : 16
=> 0,25 .16 = x2
x2 = 64 = 82 = (-8)2
=> x = 8 hoặc x = -8

\(\text{b) Ta có: MD vuông góc với BE}\)
\(\text{ BE vuông góc với EN}\)
Xét tam giác MDI và tam giác IEN ta có:
MD=EN(vì tam giác MBD = tam giác CEN)
góc MDI = góc IEN(=90 độ)
góc DMI = góc INE(cmt)
=>tam giác MDI = tam giác IEN(CGV-GN)
=>IM=IN(ctư)
=>đường thẳng BC cắt MN tại trung điểm I của MN

2) Ta có: \(\left|4-3x\right|=\left|x+\dfrac{1}{3}\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}4-3x=x+\dfrac{1}{3}\\3x-4=x+\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-4x=-\dfrac{11}{3}\\2x=\dfrac{13}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{12}\\x=\dfrac{13}{6}\end{matrix}\right.\)
3: Ta có: \(\left|5x-2\right|-\left|3x+\dfrac{1}{2}\right|=0\)
\(\Leftrightarrow\left|5x-2\right|=\left|3x+\dfrac{1}{2}\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-2=3x+\dfrac{1}{2}\\5x-2=-3x-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{5}{2}\\8x=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=\dfrac{3}{16}\end{matrix}\right.\)
4: Ta có: \(\left|2x-1\right|=x+\dfrac{4}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+\dfrac{4}{3}\left(x\ge\dfrac{1}{2}\right)\\1-2x=x+\dfrac{4}{3}\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x-x=\dfrac{4}{3}+1\\-2x-x=\dfrac{4}{3}-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\-3x=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\x=-\dfrac{1}{9}\end{matrix}\right.\)
 mn lm giup e vs
mn lm giup e vs 

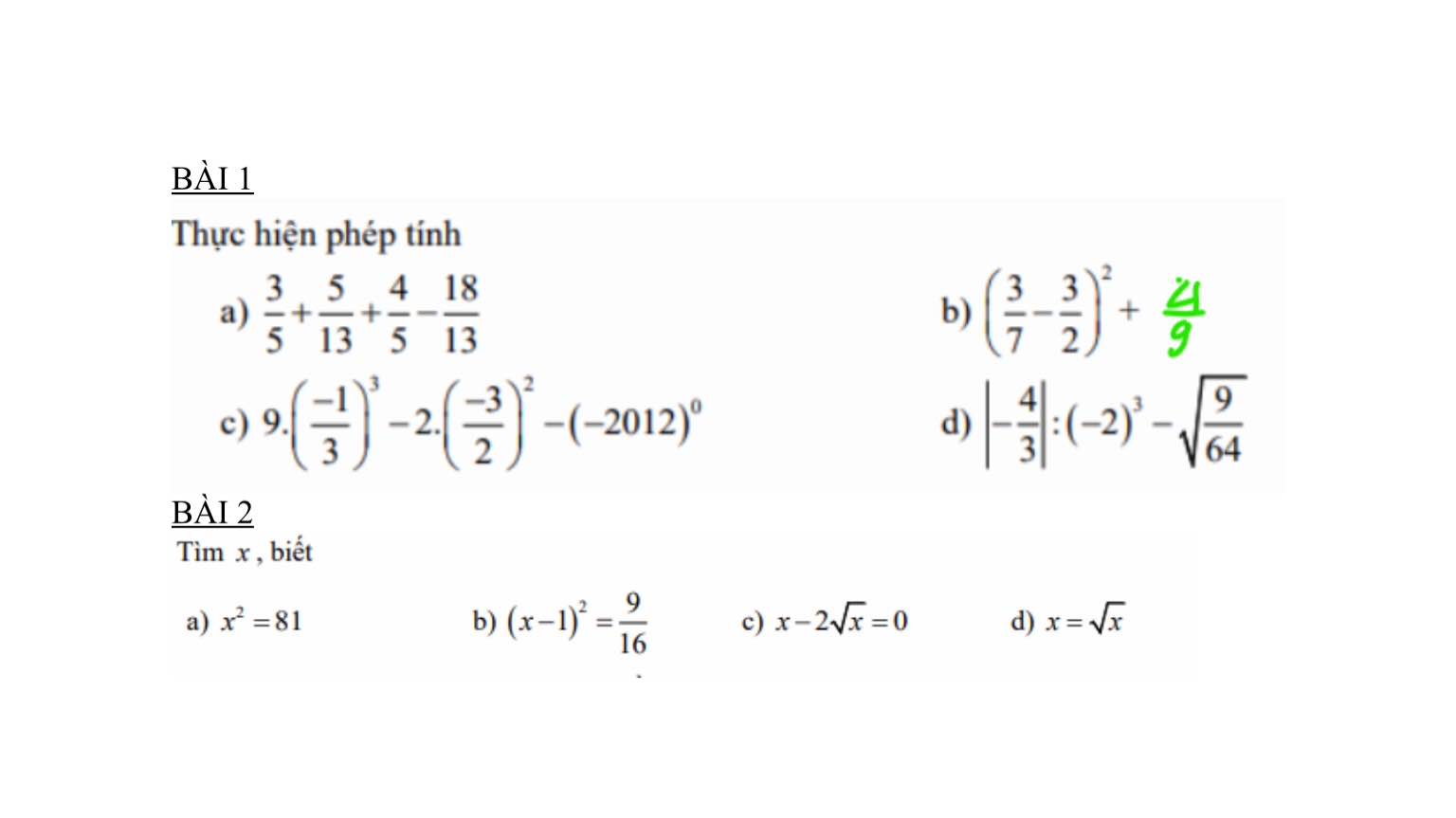 Mn lm giúp mình vs ah mình cần gấp !!!
Mn lm giúp mình vs ah mình cần gấp !!! mn lm giúp mik vs ạ.Mik đang cần gấp ạ.Nhanh ạ
mn lm giúp mik vs ạ.Mik đang cần gấp ạ.Nhanh ạ