Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Chú ý: M,A,B(O) và A M B ^ = 90 0 => ĐPCM
b, Gợi ý: Chứng minh AK và BI lần lượt là phân giác trong góc A, B của tam giác MAB

Answer:
a, \(\Delta MAB\) nội tiếp \(\left(O\right)\) có \(\widehat{AMB}=90^o\)
\(\Rightarrow AB\) là đường kính \(\left(O\right)\)
\(\Rightarrow AB\) đi qia tâm O của đường tròn
Vậy ba điểm A, O, B thẳng hàng
b, Vì I là điểm chính giữa cung nhỏ MA
\(\Rightarrow\widebat{IA}=\widebat{IM}\)
\(\Rightarrow\widehat{ABI}=\widehat{MBI}\)
\(\Rightarrow IB\) là tia phân giác của \(\widehat{MBA}\)
Vì K là điểm chính giữa cung nhỏ MB
\(\Rightarrow\widebat{KB}=\widebat{KM}\)
\(\Rightarrow\widehat{BAK}=\widehat{MAK}\)
\(\Rightarrow AK\) là tia phân giác của \(\widehat{MAK}\)
\(\Delta MAB\) có hai đường phân giác AK và IB cắt nhau tại P
Vậy P là đường tròn nội tiếp \(\Delta MAB\)

b, sửa đề AI giao BK = P
Góc MAI = BAI ( = 1/2 sđ cung MI ; cùng đường tròn tâm O ) => AI là tia phân giác MAI
tt BK là phân giác MBA
=> giao P .............đpcm
c, Ta có định lý : 2 x \(S\)MAB = MB x MA = ( MA + MB + AB ) x r
r là bán kính đường tròn nội típ
Thay số tính típ

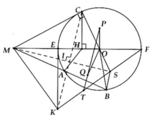
a, HS tự chứng minh
b, MH.MO = MA.MB ( = M C 2 )
=> ∆MAH:∆MOB (c.g.c)
=> M H A ^ = M B O ^
M B O ^ + A H O ^ = M H A ^ + A H O ^ = 180 0
=> AHOB nội tiếp
c, M K 2 = ME.MF = M C 2 Þ MK = MC
∆MKS = ∆MCS (ch-cgv) => SK = SC
=> MS là đường trung trực của KC
=> MS ^ KC tại trung của CK
d, Gọi MS ∩ KC = I
MI.MS = ME.MF = M C 2 => EISF nội tiếp đường tròn tâm P Þ PI = PS. (1)
MI.MS = MA.MB (= M C 2 ) => AISB nội tiếp đường tròn tâm Q Þ QI = QS. (2)
Mà IT = TS = TK (do DIKS vuông tại I). (3)
Từ (1), (2) và (3) => P, T, Q thuộc đường trung trực của IS => P, T, Q thẳng hàng

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề



a) Do MA ⊥ MB (gt)
⇒ ∠MAB = 90⁰
⇒ M, A, B thuộc đường tròn đường kính AB
Mà M, A, B thuộc (O)
⇒ O là trung điểm của AB
⇒ A, O, B thẳng hàng
b) Do I là điểm chính giữa của cung nhỏ MA (gt)
⇒ sđ cung AI = sđ cung MI
⇒ ∠ABI = ∠MBI (hai góc nội tiếp chắn hai cung bằng nhau)
⇒ BI là tia phân giác của ∠ABM
Do K là điểm chính giữa của cung MB (gt)
⇒ sđ cung BK = sđ cung MK
⇒ ∠BAK = ∠MAK (hai góc nội tiếp chắn hai cung bằng nhau)
⇒ AK là tia phân giác của ∠BAM
Mà P là giao điểm của AK và BI (gt)
⇒ P là giao điểm của ba đường phân giác của ∆MAB
⇒ P là tâm đường tròn nội tiếp ∆MAB
a.
Do \(OM=OA=R\Rightarrow\Delta OAM\) cân tại O
\(\Rightarrow\widehat{OAM}=\widehat{OMA}\Rightarrow\widehat{AOM}=180^0-\left(\widehat{OAM}+\widehat{OMA}\right)=180^0-2\widehat{OMA}\)
Tương tự, \(\Delta OBM\) cân tại O
\(\Rightarrow\widehat{BOM}=180^0-2\widehat{OMB}\)
\(\Rightarrow\widehat{AOM}+\widehat{BOM}=360^0-2\left(\widehat{OMA}+\widehat{OMB}\right)\)
\(\Rightarrow\widehat{AOM}+\widehat{BOM}=360^0-2.\widehat{AMB}=360^0-2.90^0=180^0\)
\(\Rightarrow A,O,B\) thẳng hàng
b.
Do I là điểm chính giữa cung MA \(\Rightarrow sđ\stackrel\frown{AI}=sđ\stackrel\frown{MI}\Rightarrow\widehat{ABI}=\widehat{MBI}\)
\(\Rightarrow BI\) là tia phân giác góc \(\widehat{ABM}\) (1)
Do K là điểm chính giữa cung MB \(\Rightarrow sđ\stackrel\frown{MK}=sđ\stackrel\frown{BK}\Rightarrow\widehat{MAK}=\widehat{BAK}\)
\(\Rightarrow AK\) là tia phân giác góc \(\widehat{MAB}\) (2)
(1);(2) \(\Rightarrow P\) là giao điểm 2 đường phân giác trong của tam giác MAB
\(\Rightarrow P\) là tâm đường tròn nội tiếp tam giác MAB