Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A=10^{100}+5\)
- Tận cùng A là số 5 \(\Rightarrow A⋮5\)
- Tổng các chữ số của A là \(1+5=6⋮3\Rightarrow A⋮3\) \(\)
\(\Rightarrow dpcm\)
b) \(B=10^{50}+44\)
- Tận cùng B là số 4 là số chẵn \(\Rightarrow B⋮2\)
- Tổng các chữ số của B là \(1+4+4=9⋮9\Rightarrow B⋮9\)
\(\Rightarrow dpcm\)

\(=\left(\dfrac{1}{49}-\dfrac{1}{9}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49^2}\right)=0\)

- 27/1=81/3 (Ngược lại)
- 3/9=27/81 (Ngược lại)
- 27/9=3/1 (Ngược lại)
- 81/9=27/3 (Ngược lại)
- 1/27=3/81 (Ngược lại)
\(\dfrac{1}{1}\) = \(\dfrac{3}{3}\) = \(\dfrac{9}{9}\) = \(\dfrac{27}{27}\) = \(\dfrac{81}{81}\)

chứng minh rằng
8a+6b chia hết 11 khi và chỉ khi a-2b chia hết 11
thấy cô giúp e vs ạ ! e xin cảm ơn !


Không c/m được a^4 - b^4 chia hết cho 5 đâu bạn ạ vì đơn giản không phải nó luôn đúng nhưng nếu c/m ab(a^4 - b^4) chia hết cho 5 với a, b là số nguyên thì c/m được đó bạn ạ!
~~~~~~~
Bạn biến đổi: ab(a^4 - b^4) = ab[(a^4 - 1) - (b^4 - 1)]
= ab(a - 1)(a + 1)(a² + 1) - ab(b - 1)(b + 1)(b² + 1).
Sau đó bạn xét các trường hợp của a, b như chia hết cho 5, chia 5 dư 1, -1, 2, -2 để c/m a(a - 1)(a + 1)(a² + 1) chia hết cho 5, ab(b - 1)(b + 1)(b² + 1) chia hết cho 5 => ab(a - 1)(a + 1)(a² + 1) - ab(b - 1)(b + 1)(b² + 1) chia hết cho 5 hay ab(a^4 - b^4) chia hết cho 5 (đpcm).
~~~~~~~~

\(A=2+2^2+2^3+2^4+...+2^{99}+2^{100}\)
\(\Rightarrow A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{99}+2^{100}\right)\)
\(\Rightarrow A=\left(2+2^2\right)+2^2\left(2+2^2\right)+...+2^{98}\left(2+2^2\right)\)
\(\Rightarrow A=\left(2+2^2\right)\left(1+2^2+...+2^{98}\right)\)
\(\Rightarrow A=6\left(1+2^2+...+2^{98}\right)⋮6\)

Vì abcabc = 1001 x abc
Mà 1001 lại chia hết cho 11
=> abcabc chia hết cho 11
Hội con 🐄 chúc bạn học tốt!!!
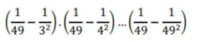
\(\overline{ab}-\overline{ba}=10.a+b-10.b-a=9\left(a-b\right)⋮9\)