Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số đo mỗi cạnh của tam giác lần lượt là x, y, z (đơn vị: m) (x, y, z \(\in\)N*)
Do mỗi cạnh của tam giác tỉ lệ với 4; 5; 8
\(\frac{x}{4}=\frac{y}{5}=\frac{z}{8}\)
Chu vi hình tam giác là 34m
=> x + y + z = 34
Theo tính chất của dãy tỉ số bằng nhau.
\(\frac{x}{4}=\frac{y}{5}=\frac{z}{8}=\frac{x+y+z}{4+5+8}=\frac{34}{17}=2\)
\(\frac{x}{4}=2\Rightarrow x=2.4=8\)
\(\frac{y}{5}=2\Rightarrow y=2.5=10\)
\(\frac{z}{8}=2\Rightarrow z=2.8=16\)
Vậy, độ dài mỗi cạnh của tam giác lần lượt là 8; 10; 16.
@Nghệ Mạt
#cua
Gọi các cạnh của tam giác lần lượt là x1, x2, x3
Theo đề bài ta có: \(\frac{x_1}{4}\), \(\frac{x_2}{5}\), \(\frac{x_3}{8}\)= \(\frac{34}{17}\)= \(2\)
Do đó:
x1 = 2.4 = 6
x2 = 2.5 = 10
x3 = 2.8 = 16
Độ dài của các cạnh lần lượt là 6, 10, 16
Chu vi của một tam giác là 36 m. Tính độ dài các cạnh của tam giác biết rằng chúng tỉ lệ với 3; 4; 5


Gọi a (m), b (m) lần lượt là chiều dài và chiều rộng của hình chữ nhật (a > b > 0)
Do chu vi của hình chữ nhật là 144 m nên:
a + b = 144 : 2 = 72 (m)
Do chiều dài và chiều rộng tỉ lệ thuận với 5; 3 nên:
a/5 = b/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a/5 = b/3 = (a + b)/(5 + 3) = 72/8 = 9
a/5 = 9 ⇒ a = 9.5 = 45
b/3 = 9 ⇒ b = 9.3 = 27
Diện tích hình chữ nhật:
45 . 27 = 1215 (m²)
Bài 1
Gọi a (m), b (m), c (m) lần lượt là độ dài ba cạnh cần tìm (a, b, c > 0)
Do chu vi tam giác là 24 m nên a + b + c = 24 (m)
Do ba cạnh tỉ lệ với 3; 4; 5 nên:
a/3 = b/4 = c/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a/3 = b/4 = c/5 = (a + b + c)/(3 + 4 + 5) = 24/12 = 2
a/3 = 2 ⇒ a = 2.3 = 6
b/4 = 2 ⇒ b = 2.4 = 8
c/5 = 2 ⇒ c = 2.5 = 10
Vậy độ dài ba cạnh của tam giác đã cho lần lượt là 3 m, 4 m, 5 m

a: Gọi độ dài ba cạnh lần lượt là a,b,c
Theo đề, ta có: a/4=b/5=c/7 và a+b+c-2a=2
Áp dụng tính chất của DTBSN, ta được:
\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c-2a}{4+5+7-2\cdot4}=\dfrac{2}{8}=\dfrac{1}{4}\)
=>a=1; b=5/4; c=7/4
b: Gọi độ dài ba cạnh lần lượt là a,b,c
Theo đề, ta có:
a/2=b/4=c/5
Áp dụng tính chất của DTSBN, ta đc:
\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{2+4+5}=\dfrac{33}{11}=3\)
=>a=6; b=12; c=15

Gọi đọ dài các cạnh lần lượt là a,b,c (a,b,c thuộc N*)
theo bài ra ta có: a/4=b/5=c/6
Áp dụng tchất dãy tỉ số bằng nhau ta có:
a/4=b/5=c/6= a+b+c/4+5+6=30(cm)/15 = 2(cm)
(chu vi là tổng đọ dài các cạnh)
=> a=8(cm)
b=10(cm)
c=12(cm)
vậy ......................................................
ủng hộ nhé các bạn

Tính độ dài các cạnh của một tam giác biết chu vi là 22cm và các cạnh của tam giác tỉ lệ với các số 2; 4; 5
Gọi 3 cạnh của tam giác lần lượt là a,b,c
Ta có : a = b = c
2 4 5
Theo tính chất dãy tỉ số bằng nhau ta có :
a = b = c = a + b + c = 22 = 2
2 4 5 2 + 4 + 5 11
+ ) a = 2 => a = 4
2
+ ) b = 2 => b = 8
4
+ ) c = 2 => c = 10
5
học tốt
7.3 a/b = c/d
=> ad = bc
ad - ac = bc - ac
a(c - d) = c(a - b)
=>a/(a - b) = c/(c - d)
7.4 ta có a/b=c/d
Áp dụng tính chất cơ bản của DTSBN, ta có
a/b=c/d nên a/c=b/d
=>(ac/bd)=(a^2)/(c^2)=(b^2)/(d^2)=( a^2 + c^2)/(b^2 + d^2)
=> ĐPCM
74 ta có x/2=y/5=x+y/2+5=-21/7=-3
=>x=-3.2=-6
y=-3.5=-15
75. ta có 7x=3y=>x/3=y/7=x-y/3-7=16/-4=-4
=>x=-4.3=-12
y=-4.7=-28

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{c-a}{5-3}=4\)
Do đó: a=12; b=16; c=20

Gọi độ dài các cạnh của tam giác lần lượt là x, y, z (cm)
Theo đề bài ta có x + y + z = 36 và
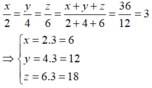
Chọn đáp án B

\(a,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c<120)
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{120}{12}=10\\ \Rightarrow \begin{cases} a=10.3=30\\ b=10.4=40\\ c=10.5=50 \end{cases} \)
Vậy ...
\(b,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c)
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{c-a}{7-3}=\dfrac{80}{4}=20\\ \Rightarrow \begin{cases} a=20.3=60\\ b=20.5=100\\ c=20.7=140 \end{cases}\\ \Rightarrow P=a+b+c=300(cm)\)
Gọi 3 cạnh tam giác : a, b, c (m) (ĐK:a, b, c > 0)
Theo bài ra, ta có : a/4 = b/5 = c/8 và a+b+c=34
Áp dụng TC dãy tỉ số bằng nhau :
\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{c}{8}=\dfrac{a+b+c}{4+5+8}=\dfrac{34}{17}=2\\ \Rightarrow\left\{{}\begin{matrix}a=2.4=8\\b=2.5=10\\c=2.8=16\end{matrix}\right.\) (TM)
Vậy ...