Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x , y , z lần lượt là độ dài các cạnh của tam giác (cm) ( x , y , z > 0 )
Chu vi của tam giác là 36 cm nên x + y + z = 36
Vì các cạnh của tam giác tỉ lệ với các số 3 , 4 , 5 nên x/3 =y/4 = z/5
Theo tính chất dãy tỉ số bằng nhau ta có :
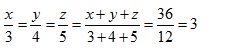
Suy ra : x = 3 . 3 = 9 (TM)
y = 4 . 3 = 12 (TM)
z = 5 . 3 = 15 (TM)
Vậy độ dài các cạnh của tam giác lần lượt là : 9cm , 12cm , 15cm .

Tính độ dài các cạnh của một tam giác biết chu vi là 22cm và các cạnh của tam giác tỉ lệ với các số 2; 4; 5
Gọi 3 cạnh của tam giác lần lượt là a,b,c
Ta có : a = b = c
2 4 5
Theo tính chất dãy tỉ số bằng nhau ta có :
a = b = c = a + b + c = 22 = 2
2 4 5 2 + 4 + 5 11
+ ) a = 2 => a = 4
2
+ ) b = 2 => b = 8
4
+ ) c = 2 => c = 10
5
học tốt
7.3 a/b = c/d
=> ad = bc
ad - ac = bc - ac
a(c - d) = c(a - b)
=>a/(a - b) = c/(c - d)
7.4 ta có a/b=c/d
Áp dụng tính chất cơ bản của DTSBN, ta có
a/b=c/d nên a/c=b/d
=>(ac/bd)=(a^2)/(c^2)=(b^2)/(d^2)=( a^2 + c^2)/(b^2 + d^2)
=> ĐPCM
74 ta có x/2=y/5=x+y/2+5=-21/7=-3
=>x=-3.2=-6
y=-3.5=-15
75. ta có 7x=3y=>x/3=y/7=x-y/3-7=16/-4=-4
=>x=-4.3=-12
y=-4.7=-28

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{c-a}{5-3}=4\)
Do đó: a=12; b=16; c=20

\(a,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c<120)
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{120}{12}=10\\ \Rightarrow \begin{cases} a=10.3=30\\ b=10.4=40\\ c=10.5=50 \end{cases} \)
Vậy ...
\(b,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c)
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{c-a}{7-3}=\dfrac{80}{4}=20\\ \Rightarrow \begin{cases} a=20.3=60\\ b=20.5=100\\ c=20.7=140 \end{cases}\\ \Rightarrow P=a+b+c=300(cm)\)

Gọi độ dài 3 cạnh của tam giác đó là x , y , z
Vì độ dài 3 cạnh của tam giác tỉ lệ lần lượt với 4 : 5 : 6 nên
x : y : z = 4 : 5 : 6
⇒x4=y5=z6⇒x4=y5=z6 và x+y+z=1500x+y+z=1500 ( vì chu vi tam giác là 1500cm )
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
x4=y5=z6=x+y+z4+5+6=150015=100x4=y5=z6=x+y+z4+5+6=150015=100
+)x4=100⇒x=400cm+)x4=100⇒x=400cm
+)y5=100⇒y=500cm

Gọi đọ dài các cạnh lần lượt là a,b,c (a,b,c thuộc N*)
theo bài ra ta có: a/4=b/5=c/6
Áp dụng tchất dãy tỉ số bằng nhau ta có:
a/4=b/5=c/6= a+b+c/4+5+6=30(cm)/15 = 2(cm)
(chu vi là tổng đọ dài các cạnh)
=> a=8(cm)
b=10(cm)
c=12(cm)
vậy ......................................................
ủng hộ nhé các bạn

Gọi độ dài 3 cạnh của tam giác lần lượt là a, b, c (a, b, c > 0; cm)
Vì độ dài 3 cạnh lần lượt tỉ lệ với 4 : 5 : 6 nên
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}\)(1)
Vì chu vi của tam giác là 1500cm nên a + b + c = 1500 (cm) (2)
Từ (1) và (2), áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{a+b+c}{4+5+6}=\frac{1500}{15}=100\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{4}=100\Rightarrow a=100.4=400cm\\\frac{b}{5}=100\Rightarrow b=100.5=500cm\\\frac{c}{6}=100\Rightarrow c=100.6=600cm\end{cases}}\)
Vậy...
Gọi độ dài 3 cạnh của tam giác đó là x , y , z
Vì độ dài 3 cạnh của tam giác tỉ lệ lần lượt với 4 : 5 : 6 nên
x : y : z = 4 : 5 : 6
\(\Rightarrow\frac{x}{4}=\frac{y}{5}=\frac{z}{6}\) và \(x+y+z=1500\) ( vì chu vi tam giác là 1500cm )
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{x}{4}=\frac{y}{5}=\frac{z}{6}=\frac{x+y+z}{4+5+6}=\frac{1500}{15}=100\)
\(+)\frac{x}{4}=100\Rightarrow x=400cm\)
\(+)\frac{y}{5}=100\Rightarrow y=500cm\)
\(+)\frac{z}{6}=100\Rightarrow z=600cm\)
Vậy độ dài 3 cạnh của tam giác đó lần lượt là 400cm , 500cm , 600cm .
Học tốt

Gọi 3 cạnh tam giác lần lượt là : a, b , c
a:b:c=3:4:5 hay
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{48}{12}=4\)
=> a = 4 . 3 = 12
=> b = 4 . 4 = 16
=> c = 5 . 4 = 20
vậy 3 cạnh có số đo lần lượt là : 12 cm , 16 cm , 20 cm
1 cạnh =9 m
1 cạnh = 12m
1 cạnh = 15m
Gọi độ dài ba cạnh của tam giác lần lượt là : a, b, c (m)
Ta có: a3a3 = b4b4 = c5c5
Theo tính chất của dãy tỉ số bằng nhau :
a3a3 = b4b4 = c5c5 =a+b+c3+4+5a+b+c3+4+5 36123612 = 3
⇒ a = 9
b = 12
c = 15
HT