Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c<120)
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{120}{12}=10\\ \Rightarrow \begin{cases} a=10.3=30\\ b=10.4=40\\ c=10.5=50 \end{cases} \)
Vậy ...
\(b,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c)
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{c-a}{7-3}=\dfrac{80}{4}=20\\ \Rightarrow \begin{cases} a=20.3=60\\ b=20.5=100\\ c=20.7=140 \end{cases}\\ \Rightarrow P=a+b+c=300(cm)\)

Gọi độ dài các cạnh của tam giác lần lượt là x, y, z (cm)
Theo đề bài ta có:
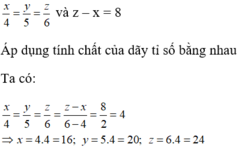
Chọn đáp án A

Gọi đọ dài 3 cạnh của tam giác là : a ; b ;c (cm)
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{c-a}{7-3}=\frac{8}{4}=2\)
a =6
b =10
c=14
Bài làm:
Gọi độ dài 3 cạnh của tam giác là: a, b, c (cm)
Vì Các cạnh của tam giác tỉ lệ với 3; 5; 7 và cạnh nhỏ nhất ngắn hơn cạnh lớn nhất 8 cm (bài cho)
\(\Rightarrow\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)(1) và c-a=8 (2)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{c-a}{7-3}=\frac{8}{4}=2\)( do có 2)
\(\Rightarrow\hept{\begin{cases}a=2\cdot3=6\\b=2\cdot5=10\\c=2\cdot7=14\end{cases}}\)
Vậy ...............

a: Gọi độ dài ba cạnh lần lượt là a,b,c
Theo đề, ta có: a/4=b/5=c/7 và a+b+c-2a=2
Áp dụng tính chất của DTBSN, ta được:
\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c-2a}{4+5+7-2\cdot4}=\dfrac{2}{8}=\dfrac{1}{4}\)
=>a=1; b=5/4; c=7/4
b: Gọi độ dài ba cạnh lần lượt là a,b,c
Theo đề, ta có:
a/2=b/4=c/5
Áp dụng tính chất của DTSBN, ta đc:
\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{2+4+5}=\dfrac{33}{11}=3\)
=>a=6; b=12; c=15

Gọi độ dài của các cạnh tam giác là a, b, c tỉ lệ với 3, 4, 5
Theo bài ra ta có:
\(a:b:c=3:4:5\) và c - a = 6
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{c-a}{5-3}=\dfrac{6}{2}=3\)
Do đó: \(\Rightarrow\left\{{}\begin{matrix}3.3=9\\4.3=12\\5.3=15\end{matrix}\right.\)
Vậy:...
Gọi độ dài các cạch của tam giác là a,b,c với các cạnh là 3,4,5
Theo đề ta có:
a:b:c=3:4:5 và c-a =6
Áp dụng tính chất của dãy số bangừ nhau ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{c-a}{5-3}=\dfrac{6}{2}=3\)
Vậy ta có như sau:
\(\dfrac{a}{3}=3\Rightarrow a=9\)
\(\dfrac{b}{4}=3\Rightarrow b=12\)
\(\dfrac{c}{5}=3\Rightarrow c=15\)

Bài làm:
* Gọi độ dài các cạnh của tam giác đó lần lượt là x, y, z.
\(\Rightarrow\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\) và x + y + z = 180 (chu vi của tam giác, định lý)
Theo tính chất dãy tỉ số bằng nhau :
\(\Rightarrow\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{180}{12}=15\left(#\right)\)
(#) \(\Rightarrow\)x = 15 . 3 = 45
(#) \(\Rightarrow\)y = 15 . 4 = 60
(#) \(\Rightarrow\)z = 15 . 5 = 75
Vậy x = 45
y = 60
z = 75
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{c-a}{5-3}=4\)
Do đó: a=12; b=16; c=20