Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hình tự vẽ nha
a) Vì tam giác ABC cân tại A
=> ABC = ACB (1)
Ta có ABC + ABD = ACB + ACE ( cùng = 1800 ) (2)
Từ (1) và (2) => ABD = ACE
Xét tam giác ABD và tam giác ACE có :
AB = AC ( gt )
ABD = ACE ( cmt )
BD = CE ( gt )
=> tam giác ABD = tam giác ACE ( c-g-c )
=> D = E
Xét tam giác BHD và tam giác CKE có :
DHB = EKC ( = 900 )
BD = CE ( gt )
D = E ( cmt )
=> tam giác BHD = tam giác CKE ( ch - gn )
=> đpcm
b) Vì tam giác ABD = tam giác ACE ( chứng minh câu a )
=> HAB = KAC ( 2 góc tương ứng )
Xét tam giác AHB và tam giác AKC có :
HAB = KAC ( cmt )
AHB = AKC ( = 900 )
AB = AC ( gt )
=> tam giác AHB = tam giác AKC ( ch - gn )
=> đpcm
c) Nối H với K
Xét tam giác ADE cân tại A ( vì AD = AE )
=> \(\widehat{D}=\frac{180^0-\widehat{DAE}}{2}\left(1\right)\)
Xét tam giác AHK cân tại A ( vì AH = AK )
\(\Rightarrow\widehat{AHK}=\frac{180^0-\widehat{DAE}}{2}\left(2\right)\)
Từ (1) và (2) => D = AHK
mà 1 góc này ở vị trí đồng vị
=> HK // DE hay HK // BC ( đpcm )
Có j lên đây hỏi nha : Group Toán Học
Xét △AMD và △DMC
AB=AC(giả thuyết)
Cạnh AM là cạnh chung
BM= CM ( M là trung điểm của cạnh BC)
=> △AMD=△DMC
Sorry bạn nhé mk chỉ bt làm câu a thui ☹
a) Vì AH = HD => EH là đg trung tuyến của tg ADE
Khi đó C thuộc đg trung tuyến EH (1)
Do tg ABC cân tại A
mà AH là đg cao của tg ABC
=> AH là đg trung trực của tg ABC
=> BH = CH
=> BH = CH = 1/2 BC
Lại do BC = CE
=> CH = 1/2 CE
hay CE = 2/3 EH (2)
Từ (1); (2) => C là trọng tâm tg ADE.
Xét ΔAHBΔAHB và ΔAHCΔAHC có :
HAHA chung
HB=HCHB=HC ( AH là đường trung tuyến của BC )
AB=ACAB=AC ( ΔABCΔABC cân tại A )
Do đó : ΔAHB=ΔAHC(c−c−c)ΔAHB=ΔAHC(c−c−c)
⇒AHBˆ=AHCˆ⇒AHB^=AHC^ ( hai góc tương ứng )
Mà AHBˆ+AHCˆ=180oAHB^+AHC^=180o ( hai góc kề bù )
⇒AHBˆ=AHCˆ=180o2=90o⇒AHB^=AHC^=180o2=90o
Xét ΔAHEΔAHE và ΔHEDΔHED có :
HEHE chung
HA=HDHA=HD ( HE là đường trung tuyến của AD )
AHEˆ=DHEˆ(=90o)AHE^=DHE^(=90o)
Do đó : ΔAHE=ΔDHEΔAHE=ΔDHE ( hai cạnh góc vuông )
⇒AEHˆ=DEHˆ⇒AEH^=DEH^ ( góc tương ứng ) (*)
Vì C là trọng tâm của ΔAEDΔAED ⇒AM⇒AM là đường trung tuyến của DE )
⇒DM=ME⇒DM=ME
Xét ΔHEDΔHED vuông tại H có : HM là đường trung tuyến nối từ đỉnh H đến DE
⇒HM=DM⇒HM=DM (1)
Lưu ý : Trong tam giác vuông , đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền . Tức HM=12DEHM=12DE. Mà 12DE=DM12DE=DM⇒HM=DM⇒HM=DM
Trở lại vào bài :
Mặt khác DM=ME(cmt)DM=ME(cmt)(2)
Từ (1) và (2) ⇒HM=ME⇒HM=ME
⇒ΔHME⇒ΔHME cân tại M
⇒MHEˆ=MEHˆ⇒MHE^=MEH^
Dễ thấy MEHˆ=HEAˆ(cmt)MEH^=HEA^(cmt) ở cái (*)
⇒MHEˆ=HEAˆ⇒MHE^=HEA^
mà hai góc này ở vị trí so le trong
⇒HM⇒HM//AEAE (đpcm)
a) Ta có : \(\widehat{ABC}=\widehat{ACB}\) (tam giác ABC cân tại A -gt)
Mà : \(\left\{{}\begin{matrix}\widehat{ABC}+\widehat{ABD}=180^o\\\widehat{ACB}+\widehat{ACE}=180^o\end{matrix}\right.\) (kề bù)
=> \(\widehat{ABD}=\widehat{ACE}\)
Xét \(\Delta ABD;\Delta ACE\) có :
\(AB=AC\) (tam giác ABC cân tại A -gt)
\(\widehat{ABD}=\widehat{ACE}\left(cmt\right)\)
\(BD=CE\left(gt\right)\)
=> \(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
b) Xét \(\Delta AHB;\Delta AKC\) có :
\(\widehat{AHB}=\widehat{AKC}\left(=90^{^O}\right)\)
\(AB=AC\) (tam giác ABC cân tại A)
\(\widehat{BAH}=\widehat{CAK}\) (do \(\Delta ABD=\Delta ACE\) -cmt)
=> \(\Delta AHB=\Delta AKC\) (cạnh huyền - góc nhọn)
c) Từ \(\Delta ABD=\Delta ACE\) - câu a
=> \(AD=AE\) (2 cạnh tương ứng)
Xét \(\Delta ADE\) có :
\(AD=AE\left(cmt\right)\)
=> \(\Delta ADE\) cân tại A (đpcm)
d) Xét \(\Delta AHK\) có :
\(AH=AK\) (do \(\Delta AHB=\Delta AKC\) - câu b)
=> \(\Delta AHK\) cân tại A
Nên ta có : \(\widehat{AHK}=\widehat{AKH}=\dfrac{180^{^O}-\widehat{DAE}}{2}\left(1\right)\)
Xét \(\Delta ADE\) cân tại A (câu c) có :
\(\widehat{ADE}=\widehat{AED}=\dfrac{180^{^O}-\widehat{DAE}}{2}\left(2\right)\)
Từ (1) và (2) => \(\widehat{AHK}=\widehat{ADE}\left(=\dfrac{180^{^O}-\widehat{DAE}}{2}\right)\)
Mà thấy : 2 góc này ở vị trí đồng vị
=> HK // DE
Lại có : \(\left\{{}\begin{matrix}B\in DE\\C\in DE\end{matrix}\right.\)
Do đó : \(\text{BC // HK (đpcm) }\)
a) Vì tam giác ABC cân tại A => góc ABC = góc ACB ( tính chất tam giác cân )
Ta có : góc ABC + góc ABD = 180o ( hai góc kề bù ) ; góc ACB + góc ACE = 180o ( hai góc kề bù ) mà góc ABC = góc ACB ( tam giác ABC cân tại A ) => góc ABD = góc ACE
Xét tam giác ABD và tam giác ACE , có :
AB = AC ( tam giác ABC cân tại A )
góc ABD = góc ACE ( chứng minh trên )
BD = CE ( gt )
=> tam giác ABD = tam giác ACE ( c-g-c )
Vậy tam giác ABD = tam giác ACE ( c-g-c )
b) Xét tam giác AHB và tam giác AKC , có :
AB = AC ( tam giác ABC cân tại A )
góc AHB = góc AKC ( = 90o )
góc HAB = góc KAC ( tam giác ABD = tam giác ACE )
=> tam giác AHB = tam giác AKC ( cạnh huyền - góc nhọn)
Vậy tam giác AHB = tam giác AKC ( cạnh huyền - góc nhọn)
c) Vì tam giác ABD = tam giác ACE ( chứng minh trên ) => AD = AE ( hai cạnh tương ứng ) => tam giác ADE cân tại A
Vậy tam giác ADE là tam giác cân
d) Vì tam giác AHB = tam giác AKC ( chứng minh trên ) => AH = AK ( hai cạnh tương ứng ) => tam giác AHK cân tại A => góc AHK = góc AKH ( tính chất tam giác cân )
Xét tam giác AHK cân tại A : góc HAK + góc AHK + góc AKH = 180o ( định lý tổng ba góc trong một tam giác )
=> góc AHK = góc AKH = 180o - góc HAK / 2 ( 1 )
Xét tam giác ADE cân tại A => góc ADE = góc AED ( tính chất tam giác cân ) : góc DAE + góc ADE + góc AED = 180o ( định lý tổng ba góc trong một tam giác )
=> góc ADE = góc AED = 180o - góc DAE / 2 ( 2 )
Từ (1) và (2) => góc AHK = góc ADE mà hai góc ở vị trí đồng vị nên HK // DE hay HK // BC (dấu hiệu nhận biết hai đường thẳng song song)
Vậy HK // BC ( đpcm )
****** Chúc bn hc tốt ***********
- Gợi ý:
Câu 1:
a) - Sửa lại đề: Tam giác ABD=Tam giác ICE (c-g-c) do có AB=AC=CI, góc ABC=góc ACB=góc ECI, BD=CE.
b) Do tam giác ABD=Tam giác ICE nên AD=IE :
AE+EI>AI=2AC=AB+AC
=>AE+AD>AB+AC.
Câu 2:
- Tam giác MBD=Tam giác NCE do góc MDB=góc CEN=900, BD=CE,
góc MBD=góc NCE. nên BM=CN
Câu 3:
- AB=AM+BM ; CI=CN+NI.
=>AM=NI.
=>AM+AN=AM+NI=AI=AB+AC.
-c/m MN>BC (c/m mệt lắm nên mình nói ngắn gọn).
MN cắt BC tại F =>MF>DF, NF>EF
MF+NF>DF+EF=DF+CF+CE=DF+CF+BD=BC =>MN>BC
\(a,\left\{{}\begin{matrix}AB=AC\\BH=HC\\AH\text{ chung}\end{matrix}\right.\Rightarrow\Delta AHB=\Delta AHC\left(c.c.c\right)\\ \Rightarrow\widehat{AHB}=\widehat{AHC}\\ \text{Mà }\widehat{AHB}+\widehat{AHC}=180^0\\ \Rightarrow\widehat{AHB}=\widehat{AHC}=90^0\\ \Rightarrow AH\perp BC\\ b,\left\{{}\begin{matrix}HM=HA\\\widehat{AHB}=\widehat{MHC}\left(đđ\right)\\BH=HC\end{matrix}\right.\Rightarrow\Delta AHB=\Delta MHC\left(c.g.c\right)\\ \Rightarrow\widehat{HBA}=\widehat{HCM}\\ \text{Mà 2 góc này ở vị trí slt nên }AB\text{//}MC\)
a) Vì \(\Delta ABC\) cân tại A
=> \(\widehat{B}=\widehat{C}\)
mà \(\widehat{ABD}+\widehat{ABC}=180^0\) (kề bù)
và \(\widehat{ACB}+\widehat{ACE}=180^0\) (kề bù)
Do đó: \(\widehat{ABD}=\widehat{ACE}\)
Xét \(\Delta ABC\) và \(\Delta ACE\) có:
AB = AC (gt)
\(\widehat{ABD}=\widehat{ACE}\) (cmt)
DB = CE (gt)
Do đó: \(\Delta ABD=\Delta ACE\left(c-g-c\right)\)
=> \(\widehat{D}=\widehat{E}\) ( hai góc tương ứng)
Xét \(\Delta DBH\) và \(\Delta ECK\) có:
\(\widehat{DHB}=\widehat{CKE}\) ( = 900)
DB = CE (gt)
\(\widehat{D}=\widehat{E}\)(cmt)
Do đó: \(\Delta DBH=\Delta ECK\) (ch -gn)
=> BH = CK (hai cạnh tương ứng)
b) Xét \(\Delta ABH\) và \(\Delta ACK\) có:
CK = BH ( cmt )
\(\widehat{AHB}=\widehat{AKC}\left(=90^0\right)\)
AB = AC (gt)
Do đó: \(\Delta ABH=\Delta ACK\) ( cạnh huyền - cạnh góc vuông)
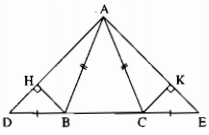
a) Vì ∆ABC cân tại A nên góc ABC =góc ACB (tính chất tam giác cân)
Ta có: góc ABC + góc ABD=180o (hai góc kề bù)
góc ACB + góc ACE=180o (hai góc kề bù)
Suy ra: góc ABD = góc ACE
Xét ∆ABD và ∆ACE, ta có:
AB = AC (gt)
góc ABD = góc ACE (chứng minh trên)
BD = CE (gt)
Suy ra: ∆ABD = ∆ACE (c.g.c)
⇒ góc D = góc E (hai góc tương ứng)
Xét hai tam giác vuông BHD và CKE, ta có:
góc BHD =góc CKE=90o
BD = CE (gt)
góc D = gócE (chứng minh trên)
Suy ra: ∆BHD = ∆CKE (cạnh huyền, góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)
Xét tam giác vuông AHB và ACK, ta có:
góc AHB = gócAKC = 90o
AB = AC (gt)
BH = CK (chứng minh trên)
Suy ra: ∆ABH = ∆ACK (cạnh huyền, cạnh góc vuông)
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
bạn tự vẽ hình nhé ì bạn đang cần gấp nên mk cx k vẽ kẻo mất thời gian
anh tự vẽ hình :
a, xét tam giác AHB và tam giác AHC có : AH chung
AB = AC do tam giác ABC cân tại A (gt)
góc AHB = góc AHC do AH | BC (gt)
=> tam giác AHB = tam giác AHC (ch - cgv)
b, tam giác ABC cân tại A (gt) => góc ABC = góc ACB (tc)
góc ABD + góc ABC = 180o (kb)
góc ACE + góc ACB = 180o (kb)
=> góc ABD = góc ACE
xét tam giác ABD và tam giác ACE có : AB = AC (câu a)
DB = CE (gt)
=> tam giác ABD = tam giác ACE (c - g - c)
=> AD = AE (đn)
=> tam giác ADE cân tại A (đn)