Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc FEQ=góc FMQ=90 độ
=>FMEQ nội tiếp
Tam I là trung điểm của FQ

A B C D E F O I J M P Q L K T
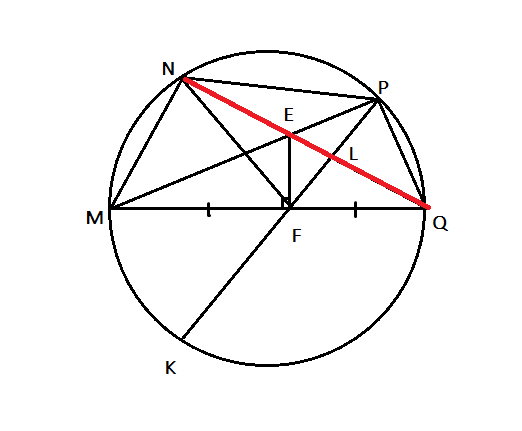
a) Vì tứ giác BFEC nội tiếp nên \(\widehat{PFB}=\widehat{ACB}=\widehat{PBF}\) suy ra \(PF=PB\)
Suy ra \(MP\perp AB\) vì MP là trung trực của BF. Do đó \(MP||CF\). Tương tự \(MQ||BE\)
b) Dễ thấy M,I,J đều nằm trên trung trực của EF cho nên chúng thẳng hàng. Vậy IJ luôn đi qua M cố định.
c) Gọi FK cắt AD tại T ta có \(FK\perp AD\) tại T. Theo hệ thức lượng \(IE^2=IF^2=IT.IL\)
Suy ra \(\Delta TIE~\Delta EIL\). Lại dễ có \(EI\perp EM\), suy ra ITKE nội tiếp
Do vậy \(\widehat{ILE}=\widehat{IET}=\widehat{IKT}=90^0-\widehat{LIK}\). Vậy \(IK\perp EL.\)

1: Xét tứ giác EAOM có \(\widehat{EAO}+\widehat{EMO}=90^0+90^0=180^0\)
nên AEMO là tứ giác nội tiếp
2: Xét tứ giác AQMP có \(\widehat{APM}=\widehat{AQM}=\widehat{PAQ}=90^0\)
nên AQMP là hình chữ nhật
=>AM cắt PQ tại trung điểm của mỗi đường
mà I là trung điểm của PQ
nên I là trung điểm của AM
=>I nằm trên đường trung trực của AM(1)
Xét (O) có
EA,EM là các tiếp tuyến
Do đó: EA=EM
=>E nằm trên đường trung trực của AM(2)
Ta có: OA=OM
=>O nằm trên đường trung trực của AM(3)
Từ (1),(2),(3) suy ra E,I,O thẳng hàng

Cho đường tròn tâm OO bán kính OAOA. Điểm CC thuộc đoạn thẳng AOAO (CC khác AA và OO). Đường thẳng vuông góc với AOAO tại CC cắt đường tròn (O)(O) tại hai điểm DD và KK. Tiếp tuyến tại DD của đường tròn (O)(O) cắt đường thẳng AOAO tại EE. Tiếp tuyến tại AA của đường tròn (O)(O) cắt đường thẳng DEDE tại FF. Gọi HH là giao điểm của hai đường thẳng FOFO và DKDK.
Chứng minh các tứ giác AFDOAFDO và AHOKAHOK là tứ giác nội tiếp.

xet tu giac AFDO co: goc FAO=FDO=90(gt)
=> tu giac AFDO noi tiep ( tong 2 goc doi dien bang 180)
vi OA vuong goc voi DK tai C (gt) va D,K thuoc (O)
=> OC la duong trung truc cua DK
=> tam giac ODK can tai O
=> goc ODK = OKD (1)
Mat khac, ta lai co F nam ngoai (O);
FA va FD lan luot la cac tiep tuyen cua (O)
=> FO vuong goc voi AD
va ta thay DC vuong goc voi OA
nen H la truc tam cua tam giac OAD
=>AH vuong goc voi OD=> AH song song voi ED
=> goc HAO=DEO (dong vi) (2)
Ta thay goc DEO= 90- goc DOE (tong 3 goc trong tam giac DOE)
va goc ODK=90- goc DOE (tong 3 goc trong tam giac DOK)
=>goc ODK=DEO (3)
Tu (1);(2);(3)=> goc OAH=OKH
=>tu giac AHOK noi tiep

a: PM\(\perp\)MQ
MQ\(\perp\)AB
Do đó: PM//AB
Xét tứ giác PMIO có
IO//MP
\(\widehat{PMI}=90^0\)
Do đó: PMIO là hình thang vuông
b: ΔMPQ vuông tại M
=>ΔMPQ nội tiếp đường tròn đường kính PQ
mà ΔMPQ nội tiếp (O)
nên O là trung điểm của PQ
=>P,Q,O thẳng hàng
c: ΔAOC vuông tại O
=>\(OA^2+OC^2=AC^2\)
=>\(R^2+R^2=\left(a\sqrt{2}\right)^2=2a^2\)
=>\(R=a\)
Kẻ OH\(\perp\)AC
=>d(O;AC)=OH
Xét ΔOAC vuông tại O có OH là đường cao
nên \(OH\cdot AC=OA\cdot OC\)
=>\(OH\cdot a\sqrt{2}=a\cdot a=a^2\)
=>\(OH=\dfrac{a}{\sqrt{2}}\)
Vậy: Khoảng cách từ O đến AC là \(\dfrac{a\sqrt{2}}{2}\)