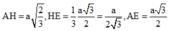Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là giao điểm của AC và BD \(\Rightarrow A_1O\perp\left(ABCD\right)\)
Gọi E là trung điểm của AD \(\Rightarrow\begin{cases}OE\perp AD\\A_1E\perp AD\end{cases}\)
Suy ra \(\widehat{A_1EO}\) là góc giữa 2 mặt phẳng \(\left(ADD_1A_1\right)\) và \(\left(ABCD\right)\) \(\Rightarrow\widehat{A_1EO}=60^o\)
Suy ra : \(A_1O=OE.\tan\widehat{A_1EO}=\frac{AB}{2}\tan\widehat{A_1EO}=\frac{a\sqrt{3}}{2}\)
Diện tích đáy \(S_{ABCD}=AB.AD=a^2\sqrt{3}\)
Thể tích \(V_{ABCD.A'B'C'D'}=S_{ABCD}.A_1O=\frac{3a^2}{2}\)
Ta có : \(B_1C||A_1D\)\(\Rightarrow B_1C||\left(A_1CD\right)\)
\(\Rightarrow d\left(B_1,\right)\left(A_1BD\right)=d\left(C,\left(A_1BD\right)\right)=CH\)
\(\Rightarrow d\left(B_1,\right)\left(A_1BD\right)=CH=\frac{CD.CB}{\sqrt{CD^2+CB^2}}=\frac{a\sqrt{3}}{2}\)

Một đường thẳng muốn vuông góc với một mặt phẳng thì phải vuông góc với 2 đường thẳng chéo nhau chứ bạn? ở ba câu trên bạn mới chứng minh nó vuông với 1 đường mà

A C D B (P) (Q)
Do \(\left(P\right)\perp\left(Q\right)\) và \(\left(P\right)\cap\left(Q\right)=\Delta\)
và \(DB\perp\left(\Delta\right)\left(DB\in\left(Q\right)\right)\)
Nên \(DB\perp\left(P\right)\Rightarrow DB\perp BC\)
Tương tự ta có :
\(CA\perp AD\)
Vì \(\widehat{CAD}=\widehat{DBC}=90^0\) nên CD chính là đường kính hình cầu ngoại tiếp tứ diện ABCD.
Gọi R là bán kính của hinh cầu này thì :
\(R=\frac{1}{2}CD\) (1)
Theo định lý Pitagoc trong 2 tam giác vuông CAD, ABD ta có :
\(CD^2=CA^2+AD^2=CA^2+BA^2+BD^2=3a^2\)
\(\Rightarrow CD=a\sqrt{3}\) (2)
Từ (1) và (2) suy ra \(R=\frac{a\sqrt{3}}{2}\)

Gọi H là hình chiếu của S lên đáy
Do \(SA=SB=SC\Rightarrow HA=HB=HC\)
\(\Rightarrow H\) là tâm đường tròn ngoại tiếp tam giác ABC
\(\Rightarrow\) H là trung điểm AC hay H là tâm đáy
\(AB=\sqrt{AC^2-BC^2}=a\sqrt{3}\)
Do H là hình chiếu S lên đáy \(\Rightarrow BH\) là hình chiếu của SB lên đáy
\(\Rightarrow\widehat{SBH}=60^0\Rightarrow SH=BH.tan60^0=a\sqrt{3}\)
\(V=\frac{1}{3}BH.AB.BC=\frac{1}{3}.a\sqrt{3}.a\sqrt{3}.a=a^3\)
Ko đáp án nào đúng?

Giải:
a) Mặt phẳng (ACD) đi qua A(5 ; 1 ; 3) và chứa giá của các vectơ (0 ; -1 ; 1)
và (-1 ; -1 ; 3).
Vectơ = (-2 ; -1 ; -1) vuông góc với mặt phẳng (ACD).
Phương trình (ACD) có dạng:
2(x - 5) + (y - 1) + (z - 3) = 0.
hay 2x + y + z - 14 = 0.
Tương tự: Mặt phẳng (BCD) qua điểm B(1 ; 6 ; 2) và nhận vectơ làm vectơ pháp tuyến.
Ta có :(4 ; -6 ; 2),
(3 ; -6 ; 4) và
= (-12 ; -10 ; -6)
Xét (6 ; 5 ; 3) thì
nên
cũng là vectơ pháp tuyến của mặt phẳng (BCD). Phương trình mặt phẳng (BCD) có dạng:
6(x - 1) + 5(y - 6) +3(z - 2) = 0
hay 6x + 5y + 3z - 42 = 0.
b) Mặt phẳng ( α ) qua cạnh AB và song song với CD thì ( α ) qua A và nhận
(-4 ; 5 ; 1) ,
(-1 ; 0 ; 2) làm vectơ chỉ phương.
Vectơ = (10 ; 9 ; 5) là vectơ pháp tuyến của ( α ).
Phương trình mặt phẳng ( α ) có dạng : 10x + 9y + 5z - 74 = 0.







Đáp án C
Hạ AH ^ (BCD) và HE ^ CD thì A E H ^ = α
Đặt AB = a ta tính được