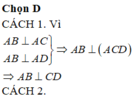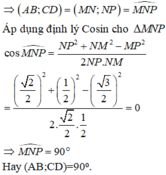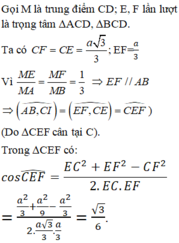Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1:
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt[3]{2-5x}+2}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{10-5x}{\left(x-2\right)\left(\sqrt[3]{2-5x}^2+2\sqrt[3]{2-5x}+4\right)}=\lim\limits_{x\rightarrow2}\dfrac{-5}{\sqrt[3]{2-5x}^2+2\sqrt[3]{2-5x}+4}=-\dfrac{5}{4}\)

Xét \(\Delta ACB\)có:
N là trung điểm BC
M là trung điểm AB
=> MN là đường trung bình của tam giác ABC
=> MN // AC
Xét tam giác ABD có:
P là trung điểm AD
M là trung điểm AB
=> MP là đường trung bình của tam giác ABD
=> MP // BD
Ta có \(\left( {AC;BD} \right) = \left( {MN;MP} \right) = \widehat {NMP} = 60^\circ \)

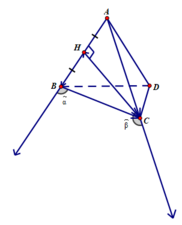
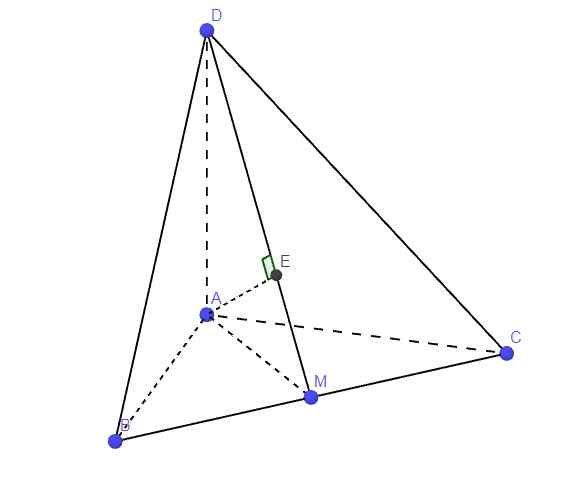
Tứ diện ABCD đều có các mặt là tam giác đều
a) Góc giữa A B → v à B C → là góc α ^ và
α ^ = 180 o - 60 o = 120 o
b) Góc giữa C H → v à A C → là β ^
H là trung điểm cạnh AB của tam giác đều ABC nên CH vừa là trung tuyến vừa là đường cao nên CH ⊥ AB
Xét tam giác vuông ACH tại H có
A C H ^ + H A C ^ = 90 o ⇒ A C H ^ = 90 o - 60 o = 30 o
Nên β ^ = 180 o - 30 o = 150 o

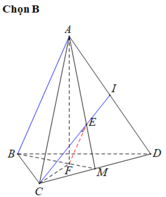
a.
Do \(AB=AC\Rightarrow\Delta ABC\) cân tại A
\(\Rightarrow AM\) là trung tuyến đồng thời là đường cao
\(\Rightarrow AM\perp BC\) (1)
Mà \(\left\{{}\begin{matrix}AD\perp AB\left(gt\right)\\AD\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(ABC\right)\Rightarrow AD\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(ADM\right)\)
b.
Từ A kẻ \(AE\perp DM\) (E thuộc DM)
Do \(BC\perp\left(ADM\right)\Rightarrow BC\perp AE\)
\(\Rightarrow AE\perp\left(BCD\right)\Rightarrow AE=d\left(A;\left(BCD\right)\right)\)
\(BC=\sqrt{AB^2+AC^2}=5\sqrt{2}\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5\sqrt{2}}{2}\)
Hệ thức lượng trong tam giác vuông ADM:
\(AE=\dfrac{AD.AM}{\sqrt{AD^2+AM^2}}=\dfrac{5\sqrt{3}}{3}\)
c.
Do \(AD\perp\left(ABC\right)\) theo cmt \(\Rightarrow AM\) là hình chiếu vuông góc của DM lên (ABC)
\(\Rightarrow\widehat{DMA}\) là góc giữa DM và (ABC)
\(tan\widehat{DMA}=\dfrac{AD}{AM}=\sqrt{2}\Rightarrow\widehat{DMA}\approx54^044'\)

b1: cho hình hộp ABCDA'B'C'D' có tất cả các mặt đều là hinh fthoi cạnh a. góc BAA'= góc BAD = góc DAA' = 60 độ. tính độ dài AC
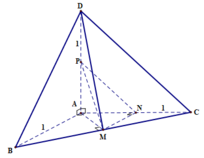
b2: cho tứ diện ABCD có CD=1/2 AB. I,J,K lần lượt là trung điểm của BC,AC,BD. biết JK=5/6AB. tính góc giữa CD với ỊJ và AB