Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi E là trung điểm của AB
ΔABC đều nên CE vuông góc AB
ΔABD đều nên DE vuông góc AB
=>AB vuông góc (CDE)
=>AB vuông góc CD
b: Xét ΔCAB có CN/CB=CM/CA
nên MN//AB và MN=1/2AB
Xét ΔDAB có DQ/DA=DP/DB
nên PQ//AB và PQ/AB=DQ/DA=1/2
=>MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔADC có AQ/AD=AM/AC
nên QM//DC
=>QM vuông góc AB
=>QM vuông góc QP
=>MNPQ là hình chữ nhật

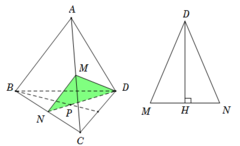
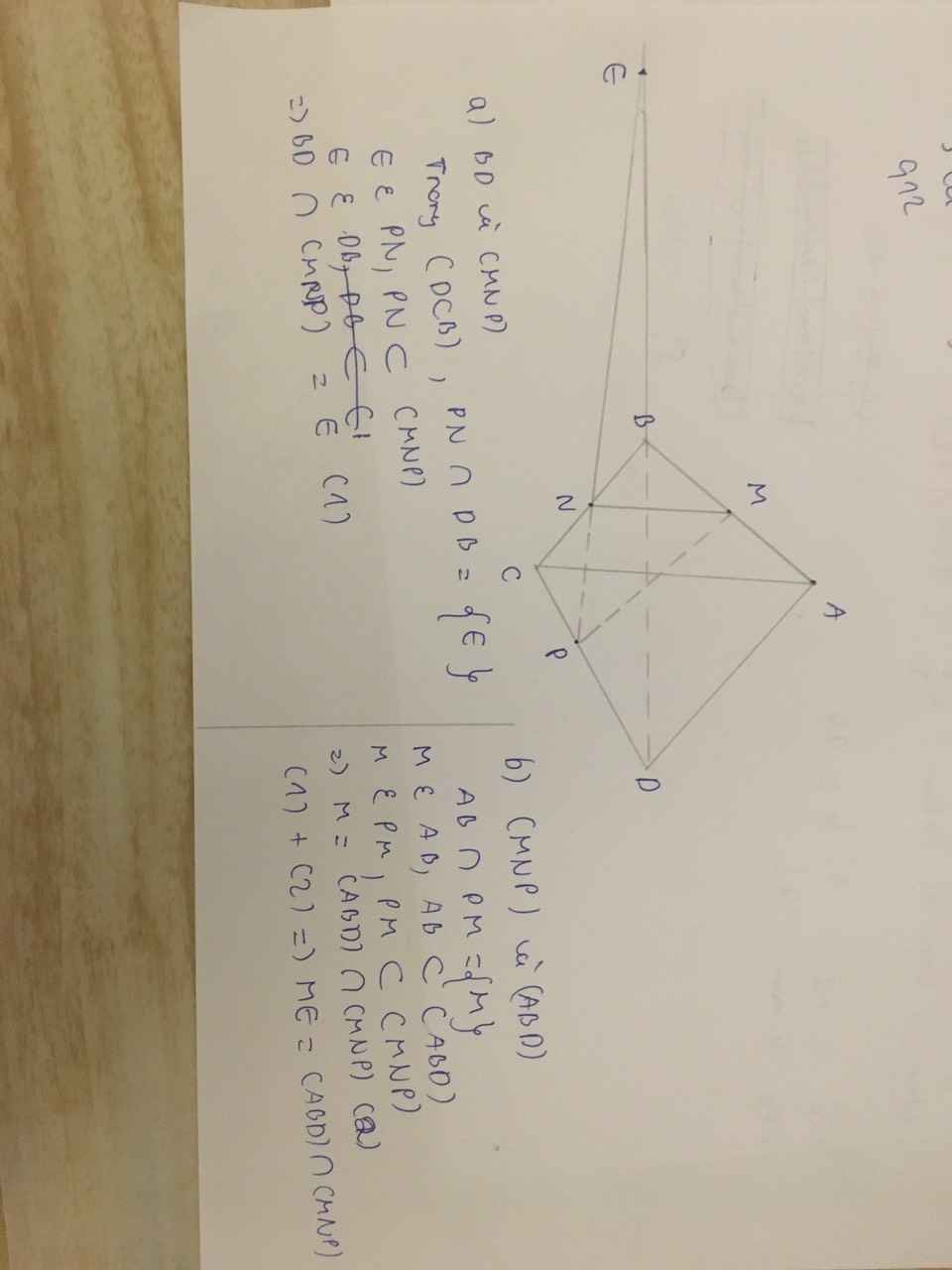
Trong tam giác BCD có: Plà trọng tâm, N là trung điểm BC .
Suy ra N; P; D thẳng hàng.
Vậy thiết diện là tam giác MND..
Xét tam giác MND, ta có M N = A B 2 = a ; D M = D N = A D 3 2 = a 3
Do đó tam giác MND cân tại D.
Gọi H là trung điểm MN suy ra DH và MN vuông góc với nhau..
Diện tích tam giác S Δ M N D = 1 2 M N . D H = 1 2 M N . D M 2 − M H 2 = a 2 11 4
Chọn C.

Do ABC cân \(\Rightarrow AM\perp BC\)
Mà \(DA\perp\left(ABC\right)\Rightarrow DA\perp BC\)
\(\Rightarrow BC\perp\left(ADM\right)\Rightarrow BC\perp AH\)
\(\Rightarrow AH\perp\left(BCD\right)\)
b.
Gọi N là trung điểm AB \(\Rightarrow MN\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}MN||AC\\MN=\dfrac{1}{2}AC=\dfrac{a}{2}\end{matrix}\right.\)
\(\Rightarrow\widehat{\left(AC;DM\right)}=\widehat{\left(MN;DM\right)}=\widehat{DMN}\)
\(DN=\sqrt{AD^2+AN^2}=\sqrt{AD^2+\left(\dfrac{AB}{2}\right)^2}=\dfrac{a\sqrt{89}}{10}\)
\(AM=\sqrt{AB^2-\left(\dfrac{BC}{2}\right)^2}=\dfrac{4a}{5}\Rightarrow DM=\sqrt{AD^2+AM^2}=\dfrac{4a\sqrt{2}}{5}\)
Định lý hàm cos cho tam giác DMN:
\(cos\widehat{DMN}=\dfrac{DM^2+MN^2-DN^2}{2DM.MN}=\dfrac{2\sqrt{2}}{5}\)
\(\Rightarrow\widehat{DMN}\approx55^033'\)
c.
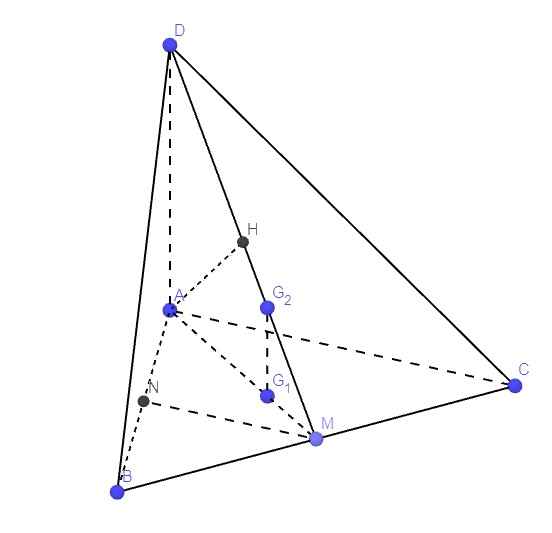
M là trung điểm BC nên hiển nhiên \(G_1\) nằm trên AM và \(G_2\) nằm trên DM
Do \(G_1\) là trọng tâm ABC \(\Rightarrow\dfrac{AG_1}{AM}=\dfrac{2}{3}\Rightarrow\dfrac{MG_1}{AM}=\dfrac{1}{3}\)
Do \(G_2\) là trọng tâm DBC \(\Rightarrow\dfrac{DG_2}{DM}=\dfrac{2}{3}\Rightarrow\dfrac{MG_2}{DM}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{MG_1}{AM}=\dfrac{MG_2}{DM}\Rightarrow G_1G_2||DA\) (Talet đảo)
Mà \(DA\perp\left(ABC\right)\Rightarrow G_1G_2\perp\left(ABC\right)\)

b1: cho hình hộp ABCDA'B'C'D' có tất cả các mặt đều là hinh fthoi cạnh a. góc BAA'= góc BAD = góc DAA' = 60 độ. tính độ dài AC
b2: cho tứ diện ABCD có CD=1/2 AB. I,J,K lần lượt là trung điểm của BC,AC,BD. biết JK=5/6AB. tính góc giữa CD với ỊJ và AB

Đáp án D
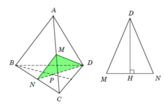
Trong tam giác BCD có: P là trọng tâm, N là trung điểm BC . Suy ra N , P , D thẳng hàng.
Vậy thiết diện là tam giác MND .
Xét tam giác MND , ta có ![]()
![]()
Do đó tam giác MND cân tại D .
Gọi H là trung điểm MN suy ra DH ⊥ MN
Diện tích tam giác ![]()
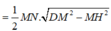
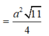
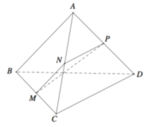
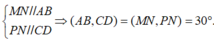
Xét \(\Delta ACB\)có:
N là trung điểm BC
M là trung điểm AB
=> MN là đường trung bình của tam giác ABC
=> MN // AC
Xét tam giác ABD có:
P là trung điểm AD
M là trung điểm AB
=> MP là đường trung bình của tam giác ABD
=> MP // BD
Ta có \(\left( {AC;BD} \right) = \left( {MN;MP} \right) = \widehat {NMP} = 60^\circ \)