Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Do tất cả các cạnh bằng a nên các mặt bên đều là hình thoi.
Mà \(\widehat{BAA'}=\widehat{BAD}=\widehat{DAA'}=60^0\Rightarrow A'B=A'D=AA'=BD=a\)
\(\Rightarrow\) Hình chiếu vuông góc H của A' lên (ABCD) là tâm tam giác đều ABD
\(AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\) ; \(AC=a\sqrt{3}\)
\(cos\widehat{A'AC}=\dfrac{AH}{AA'}=\dfrac{\sqrt{3}}{3}\Rightarrow cos\widehat{ACC'}=-\dfrac{\sqrt{3}}{3}\)
Áp dụng định lý hàm cos cho tam giác ACC':
\(AC'=\sqrt{AC^2+C'C^2-2AC.C'C.cos\widehat{ACC'}}=a\sqrt{6}\)
a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)
Chọn D.
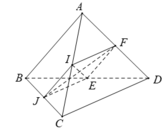
+) Từ giả thiết ta có:
- IJ là đường trung bình của tam giác ABC nên: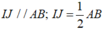 
- EF là đường trung bình của tam giác ABD nên:
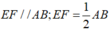
- Suy ra: tứ giác IJEF là hình bình hành (1)
- Lại có: IF là đường trung bình của tam giác ACD nên:
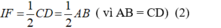
- Từ (1) và (2) suy ra: tứ giác IJEF là hình thoi.
⇒ IE ⊥ JF (tính chất hai đường chéo của hình thoi).
⇒ Do đó, góc giữa hai đường thẳng IE và JF là: 90°.
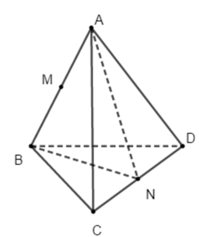
Các tam giác ABC và ABD là tam giác đều ⇒ tam giác ACD cân
⇒ BN ⊥ CD và AN ⊥ CD ⇒ góc ANB là góc của hai mặt phẳng (ACD) và (BCD)
Đáp án B
Ta có CD ⊥ (ABN) (do BN ⊥ CD và AN ⊥ CD) ⇒ (BCD) ⊥ (ABN)
Đáp án C
1. Do \(EG||AC\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)}=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}\)
Mà \(AF=AC=CF=AB\sqrt{2}\Rightarrow\Delta ACF\) đều
\(\Rightarrow\widehat{FAC}=60^0\)
2.
Do I;J lần lượt là trung điểm SC, BC \(\Rightarrow IJ\) là đường trung bình tam giác SBC
\(\Rightarrow IJ||SB\)
Lại có \(CD||BA\Rightarrow\widehat{\left(IJ;CD\right)}=\widehat{SB;BA}=\widehat{SBA}=60^0\) (do các cạnh của chóp bằng nhau nên tam giác SAB đều)
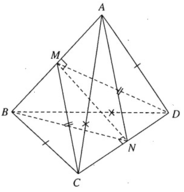
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó MN ⊥ CD vì N là trung điểm của CD. Tương tự ta chứng minh được NA = NB và suy ra MN ⊥ AB. Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.
b1: cho hình hộp ABCDA'B'C'D' có tất cả các mặt đều là hinh fthoi cạnh a. góc BAA'= góc BAD = góc DAA' = 60 độ. tính độ dài AC
b2: cho tứ diện ABCD có CD=1/2 AB. I,J,K lần lượt là trung điểm của BC,AC,BD. biết JK=5/6AB. tính góc giữa CD với ỊJ và AB