Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

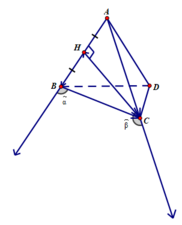
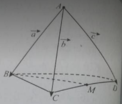
Tứ diện ABCD đều có các mặt là tam giác đều
a) Góc giữa A B → v à B C → là góc α ^ và
α ^ = 180 o - 60 o = 120 o
b) Góc giữa C H → v à A C → là β ^
H là trung điểm cạnh AB của tam giác đều ABC nên CH vừa là trung tuyến vừa là đường cao nên CH ⊥ AB
Xét tam giác vuông ACH tại H có
A C H ^ + H A C ^ = 90 o ⇒ A C H ^ = 90 o - 60 o = 30 o
Nên β ^ = 180 o - 30 o = 150 o

Tao có: \(\overrightarrow{BC}.\overrightarrow{AD}=\overrightarrow{BC}\left(\overrightarrow{DC}+\overrightarrow{CA}\right)=\overrightarrow{CB}.\overrightarrow{CD}-\overrightarrow{CB}.\overrightarrow{CA}\)
\(=\frac{1}{2}\left(CB^2+CD^2-BD^2\right)-\frac{1}{2}\left(CB^2+CA^2-AB^2\right)\)
\(=\frac{1}{2}\left(AB^2+CD^2-BD^2-CA^2\right)\)
\(\Rightarrow\cos\left(\overrightarrow{BC},\overrightarrow{DA}\right)=\frac{1}{2}.\frac{c^2+c'^2-b^2-b'^2}{2aa'}\)

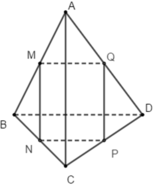
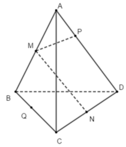
Có thể loại các phương án A, B và D vì các cặp ba vecto ( M P → , M B → , v à Q C → ) , ( M P → , M N → , P D → ) và ( M P → , M N → v à Q C → ) đều không đồng phẳng.
Phương án C đúng vì : M P → = M A → + A P → = M A → - m P D →
Đáp án C