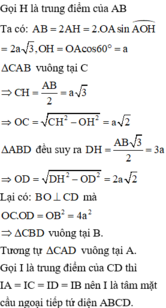Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A

Phương pháp:
Cách giải:


Mà AH vuông góc (BCD) nên AH là trục của mặt phẳng (BCD).
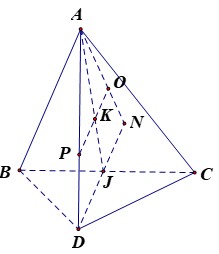
Gọi K là trung điểm AD, kẻ OK vuông góc với AD, O thuộc AH


Đáp án A.
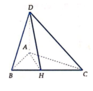
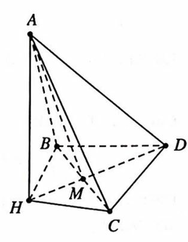
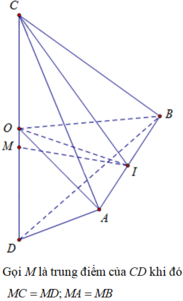
Từ dữ liệu đề bài ta thấy A B 2 + A C 2 = B C 2 ⇒ tam giác ABC vuông tại A.
Trong mặt phẳng A B C kẻ A H ⊥ B C tại H.
Ta có D A ⊥ B C A H ⊥ B C D A ∈ D A H ; A H ∈ D A H D A ∩ A H = A ⇒ D H ⊥ B C (định lý ba đường vuông góc).
Ta có A B C ∩ D B C = B C A H ⊥ B C ; D H ⊥ B C A H ∈ A B C ; D H ∈ D B C ⇒ A B C , D B C ^ = A H D ^ .
Ta có A H = A B . A C B C = 3 a .4 a 5 a = 12 a 5 .
Tam giác ADH vuông tại A.
⇒ tan A H D ^ = D A A H = 3. V A B C D S A B C 12 a 5 = 3.24 3 a 3 15. 1 2 .3 a .4 a 12 a 5 = 3 3
⇒ A H D ^ = 30 °
Vậy ta chọn A.

Đáp án là B

Gọi K là trọng tâm tam giác ABC, N đỗi xứng với D qua J, qua K kẻ KO song song với DN ta có O là tâm mặt cầu cần xác định.
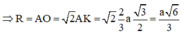

Đáp án là B.

B C = A B 2 = 2 a 2 .Gọi H là trung điểm BC ta có:
A H ⊥ B C B C = A B C ∩ D B C A B C ⊥ D B C ⇒ A H ⊥ D B C
kẻ H E ⊥ D C , H K ⊥ A E (1)
D C ⊥ H E D C ⊥ A H ( d o A H ⊥ D B C ⊂ D C ) ⇒ D C ⊥ A H E ⇒ D C ⊥ H K 2
từ 1 & 2 H K ⊥ A D C ⇒ d H ; A D C = H K
d B ; A D C = 2 d H ; A D C = 2 A H . H E A H 2 + H E 2 = 2 6 3
A H = B C 2 , H E = A B 2 ; A H = B C 2 = a 2 , H E = B C 2 = a