Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
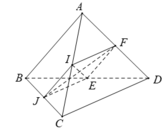
+) Từ giả thiết ta có:
- IJ là đường trung bình của tam giác ABC nên: 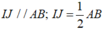
- EF là đường trung bình của tam giác ABD nên:
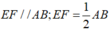
- Suy ra: tứ giác IJEF là hình bình hành (1)
- Lại có: IF là đường trung bình của tam giác ACD nên:
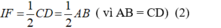
- Từ (1) và (2) suy ra: tứ giác IJEF là hình thoi.
⇒ IE ⊥ JF (tính chất hai đường chéo của hình thoi).
⇒ Do đó, góc giữa hai đường thẳng IE và JF là: 90°.

Đáp án C
Qua M vẽ đường thẳng song song với AB cắt AC tại P và vẽ đường thẳng song song với CD cắt BD tại Q. Ta có mp (MNPQ) song song với cả AB và CD. Từ đó
![]()
Áp dụng tính chất đường trung bình trong tam giác (do M, N là các trung điểm) ta suy ra được MP = MQ = NP = a hay tứ giác MPNQ là hình thoi.
Tính được
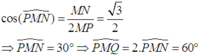

Ta có N là trung điểm của BC
Suy ra A B → + A C → = 2 A N →
Lại có: A D → = 2 A Q → (Q là trung điểm của AD)
Do đó A B → + A C → + A D → = 2 A N → + 2 A Q → = 2 A N → + A Q → (1)
Tạ lại có G là trọng tâm của tứ diện ABCD nên G là trung điểm của NQ (tính chất trọng tâm của tứ diện) ⇒ A N → + A Q → = 2 A G → (2)
Từ (1) và (2) suy ra A B → + A C → + A D → = 4 A G → .
Đáp án A

b1: cho hình hộp ABCDA'B'C'D' có tất cả các mặt đều là hinh fthoi cạnh a. góc BAA'= góc BAD = góc DAA' = 60 độ. tính độ dài AC
b2: cho tứ diện ABCD có CD=1/2 AB. I,J,K lần lượt là trung điểm của BC,AC,BD. biết JK=5/6AB. tính góc giữa CD với ỊJ và AB

a) Chú ý rằng I, J, K thẳng hàng vì chúng cùng thuộc giao tuyến của hai mặt phẳng (CBD) và (C'B'D')
b) 4. Vì 4 điểm không đồng phẳng sẽ tạo nên 1 tứ diện => có 4 mặt
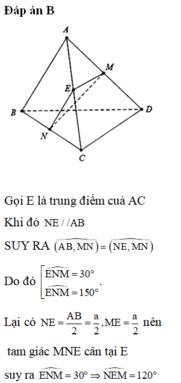
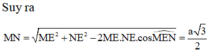

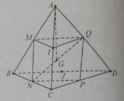

- Gọi M, N lần lượt là trung điểm AC, BC.
+) Tam giác ACD có MJ là đường trung bình của tam giác nên :
+) Tam giác BCD có NI là đường trung bình của tam giác nên:
Tương tự, ta có: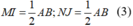
Mà theo giả thiết: AB = CD = a (4)
Từ (1), (2), (3) và (4) suy ra:
Do đó, tứ giác MJNI là hình thoi ( tính chất hình thoi).
- Gọi O là giao điểm của MN và IJ, ta có:
- Xét ΔMIO vuông tại O, ta có: