


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Xét tam giác AED và tam giác CEF có:
AE = CE (E là trung điểm của AC)
AED = CEF (2 góc đối đỉnh)
ED = EF (E là trung điểm của DF)
=> Tam giác AED = Tam giác CEF (c.g.c)
=> AD = CF (2 cạnh tương ứng) mà AD = DB (D là trung điểm của AB) => DB = CF
ADE = CFE (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => AD // CF
Xét tam giác BDC và tam giác FCD có:
BD = FC (chứng minh trên)
BDC = FCD (2 góc so le trong, AD // CF)
CD chung
=> Tam giác BDC = Tam giác FCD (c.g.c)
=> BCD = FDC (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => DE // BC
BC = FD (2 cạnh tương ứng) mà DE = 1/2 FD (E là trung điểm của FD) => DE = 1/2 BC
Xét tam giác AED và tam giác CEF có:
AE = CE (E là trung điểm của AC)
AED = CEF (2 góc đối đỉnh)
ED = EF (E là trung điểm của DF)
=> Tam giác AED = Tam giác CEF (c.g.c)
=> AD = CF (2 cạnh tương ứng) mà AD = DB (D là trung điểm của AB) => DB = CF
ADE = CFE (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => AD // CF
Xét tam giác BDC và tam giác FCD có:
BD = FC (chứng minh trên)
BDC = FCD (2 góc so le trong, AD // CF)
CD chung
=> Tam giác BDC = Tam giác FCD (c.g.c)
=> BCD = FDC (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => DE // BC
BC = FD (2 cạnh tương ứng) mà DE = 1/2 FD (E là trung điểm của FD) => DE = 1/2 BC

Xét tam giác AED và tam giác CEF có:
AE = CE (E là trung điểm của AC)
AED = CEF (2 góc đối đỉnh)
ED = EF (E là trung điểm của DF)
=> Tam giác AED = Tam giác CEF (c.g.c)
=> AD = CF (2 cạnh tương ứng) mà AD = DB (D là trung điểm của AB) => DB = CF
ADE = CFE (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => AD // CF
Xét tam giác BDC và tam giác FCD có:
BD = FC (chứng minh trên)
BDC = FCD (2 góc so le trong, AD // CF)
CD chung
=> Tam giác BDC = Tam giác FCD
=> BCD = FDC (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => DE // BC
BC = FD (2 cạnh tương ứng) mà DE = 12FD (E là trung điểm của FD) => DE = 1/2BC
a/Xét ΔAED va ΔCEF có:
AE=CE(vì E là trung điểm của AC)
∠AED=∠CEF(đối đỉnh)
ED=EF(vì E là trung điểm của DF)
nên: ΔAED=ΔCEF
do đó: AD=CF
mà AD=BD (vì D là trung điểm của AB)
vậy BD=CF
b/Ta có: ∠EAD=∠ECF(vì ΔAED=ΔCEF)
mà hai góc này ở vị trí so le trong
nên AB//CF
Ta có:AB//CF(cmt)
nên ∠BDC=∠FCD (hai góc so le trong)
Xét: ΔBDC và ΔFCD có:
DC là cạnh chung
∠BDC=∠FCD(cmt)\
DB=CF(cmt)
nên ΔBDC=ΔFCD(c-g-)
c/Ta có: ∠BCD=∠FDC(vì ΔBDC=ΔFCD)
mà hai góc này ở vị trí so le trong
nên DE//BC
Ta có: DE=1/2DF=12DF(vì E là trung điểm của DF)
mà DF=CB(vì ΔFCD=ΔBDC)
vậy DE=1/2CB

B,D,C là 3 điểm thẳng hàng mà tam giác sao đc đề sai r kìa -.- DE giao BC song song sao đc ?
câu c bn tự lm nha
xét tam giác AED và tam giác CEF ta có
AE=CE ( giả thiết)
DE=EF ( gt )
góc AED = góc FEC ( đối đỉnh)
suy ra tam giác AED=tam giác CEF( c-g-c)
=> AD =CF
=> ra BD = CF( cùng bằng AD)
b) ta có tam giác AED = tam giác CEF ( cmt)
=> góc ADE = góc EFC mà hai góc này nằm ở vị trí sole tròn nên AB song song với CF => góc BDC = góc FCD
xét tam giác BDC và tam giác FCD ta có
CD cạnh chung
DB=CF ( theo câu a)
góc BDC=góc FCD
=>> tam giác BDC = tam giác FCD ( c-g-c)
đúng 99 % đs hình bn tự vẽ nha với câu c mình ko biết lm ahihi

a) Xét t/g FEC và t/g DEA có:
FE = DE (gt)
FEC = DEA ( đối đỉnh)
EC = EA (gt)
Do đó, t/g FEC = t/g DEA (c.g.c)
=> FC = DA (2 cạnh tương ứng)
Mà DA = DB (gt) nên FC = DB (đpcm)
b) t/g FEC = t/g DEA (câu a)
=> FCE = DAE (2 góc tương ứng)
Mà FCE và DAE là 2 góc so le trong nên FC // AD hay FC // AB
Xét t/g BDC và t/g FCD có:
BD = FC (câu a)
BDC = FCD (so le trong)
CD là cạnh chung
Do đó, t/g BDC = t/g FCD (c.g.c) (đpcm)
c) t/g BDC = t/g FCD (câu b) => BC = FD (2 cạnh tương ứng)
BCD = FDC (2 góc tương ứng)
Mà DE = 1/2FD (gt)
BCD và FDC là 2 góc so le trong nên DE // BC; DE = 1/2BC (đpcm)

Cái này là ở bài: Đường trung bình của tam giác, sách lớp 8 tập 1 đó bạn
Bạn kiếm về và xem nha

Giải
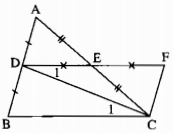
a) Xét ∆ADE và ∆CFE, ta có:
AE = CE (gt)
ˆAED = CEF^ (đối đỉnh)
DE = FE(gt)
Suy ra: ∆ADE = ∆CFE (c.g.c)
⇒⇒ AD = CF (hai cạnh tương ứng)
Mà AD = DB (gt)
Vậy: DB = CF
b) Ta có: ∆ADE = ∆CFE (chứng minh trên)
⇒ˆADE = CFE^ (2 góc tương ứng)
⇒⇒ AD // CF (vì có cặp góc so le trong bằng nhau)
Hay AB // CF
Xét ∆DBC = ∆CDF, ta có:
BD = CF (chứng minh trên)
ˆBDC = ˆFCD (hai góc so le trong vì CF // AB)
DC cạnh chung
Suy ra: ∆BDC = ∆FCD(c. g. c)
c) Ta có: ∆BDC = ∆FCD (chứng minh trên)
Suy ra: ˆC1 = ˆD1 (hai góc tương ứng)
Suy ra: DE // BC (vì có hai góc so le trong bằng nhau)
\(\Delta\)BDC = ∆FCD => BC = DF (hai cạnh tương ứng)
Mà DE = 1 : 2 . DF(gt). Vậy DE = 1 : 2 . BC
a/Xét ΔAED va ΔCEF có:
AE=CE(vì E là trung điểm của AC)
∠AED=∠CEF(đối đỉnh)
ED=EF(vì E là trung điểm của DF)
nên: ΔAED=ΔCEF(c-g-c)
do đó: AD=CF
mà AD=BD (vì D là trung điểm của AB)
vậy BD=CF
b/Ta có: ∠EAD=∠ECF(vì ΔAED=ΔCEF)
mà hai góc này ở vị trí so le trong
nên AB//CF
Ta có:AB//CF(cmt)
nên ∠BDC=∠FCD (hai góc so le trong)
Xét: ΔBDC và ΔFCD có:
DC là cạnh chung
∠BDC=∠FCD(cmt)\
DB=CF(cmt)
nên ΔBDC=ΔFCD(c-g-)
c/Ta có: ∠BCD=∠FDC(vì ΔBDC=ΔFCD)
mà hai góc này ở vị trí so le trong
nên DE//BC
Ta có: \(DE=\dfrac{1}{2}DF\)(vì E là trung điểm của DF)
mà DF=CB(vì ΔFCD=ΔBDC)
vậy \(DE=\dfrac{1}{2}CB\)
A B C F E D