Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mặt cầu (S) có tâm I (1;0;-2) và bán kính R=2.
Đường thẳng d đi qua điểm N (2; 0; m-1) và có véc tơ chỉ phương ![]()
Điều kiện để d cắt (S) tại hai điểm phân biệt là d (I; (d))<R
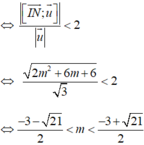
Khi đó, tiếp diện của (S) tại A và B vuông góc với IA và IB nên góc giữa chúng là góc (IA;IB).

Vậy T= {-3;0}. Tổng các phần tử của tập hợp T bằng -3.

\(f'\left(x\right)=m^2x^4-mx^2+20x-\left(m^2-m-20\right)\)
Để hàm số đồng biến trên \(ℝ\)thì \(f'\left(x\right)\ge0,\)với mọi \(x\inℝ\).
Mà ta thấy \(f'\left(-1\right)=m^2-m-20-\left(m^2-m-20\right)=0\)
do đó \(x=-1\)là một điểm cực trị của hàm số \(f'\left(x\right)\).
Ta có: \(f''\left(x\right)=4m^2x^3-2mx+20\)
\(f''\left(-1\right)=0\Leftrightarrow-4m^2+2m+20=0\Leftrightarrow\orbr{\begin{cases}m=\frac{5}{2}\\m=-2\end{cases}}\).
Thử lại.
Với \(m=\frac{5}{2}\): \(f''\left(x\right)=25x^3-5x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\)
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Với \(m=-2\): \(f''\left(x\right)=16x^3+4x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\).
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Vậy tổng các giá trị của \(m\)là: \(\frac{5}{2}+\left(-2\right)=\frac{1}{2}\).
Chọn D.

Đặt \(z=x+yi\Rightarrow w=\dfrac{1}{\sqrt{x^2+y^2}-x-yi}=\dfrac{\sqrt{x^2+y^2}-x+yi}{\left(\sqrt{x^2+y^2}-x\right)^2+y^2}\)
\(\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{\left(\sqrt{x^2+y^2}-x\right)^2+y^2}=\dfrac{1}{8}\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{2x^2+2y^2-2x\sqrt{x^2+y^2}}=\dfrac{1}{8}\)
\(\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{\sqrt{x^2+y^2}\left(\sqrt{x^2+y^2}-x\right)}=\dfrac{1}{4}\Rightarrow\dfrac{1}{\sqrt{x^2+y^2}}=\dfrac{1}{4}\)
\(\Rightarrow x^2+y^2=16\)
\(\Rightarrow\) Tập hợp \(z_1;z_2\) là đường tròn tâm O bán kính \(R=4\)
Gọi M, N lần lượt là điểm biểu diễn \(z_1;z_2\), do \(\left|z_1-z_2\right|=2\Rightarrow MN=2\)
Gọi \(P\left(0;5\right)\) và Q là trung điểm MN
\(\Rightarrow P=MP^2-NP^2=\overrightarrow{MP}^2-\overrightarrow{NP}^2=\left(\overrightarrow{MP}-\overrightarrow{NP}\right)\left(\overrightarrow{MP}+\overrightarrow{NP}\right)\)
\(=2\overrightarrow{MN}.\overrightarrow{PQ}=2\overrightarrow{MN}\left(\overrightarrow{PO}+\overrightarrow{OQ}\right)=2\overrightarrow{MN}.\overrightarrow{PO}=2MN.PO.cos\alpha\)
Trong đó \(\alpha\) là góc giữa \(MN;PO\)
Do MN, PO có độ dài cố định \(\Rightarrow P_{max}\) khi \(cos\alpha_{max}\Rightarrow\alpha=0^0\Rightarrow MN||PO\)
Mà MN=2 \(\Rightarrow M\left(\sqrt{15};-1\right);N\left(\sqrt{15};1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{PM}=\left(\sqrt{15};-6\right)\\\overrightarrow{PN}=\left(\sqrt{15};-4\right)\end{matrix}\right.\)
\(\Rightarrow P_{max}=PM^2-PN^2=15+36-\left(15+16\right)=20\)