Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) y=x+3x+1y=x+3x+1 có tập xác định : R\{-1}
y′=−2(x+1)2<0,∀x≠−1y′=−2(x+1)2<0,∀x≠−1
Tiệm cận đứng: x = -1
Tiệm cận ngang: y = 1
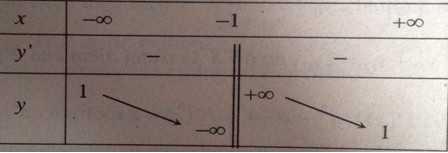
Bảng biến thiên:
Đồ thị hàm số:
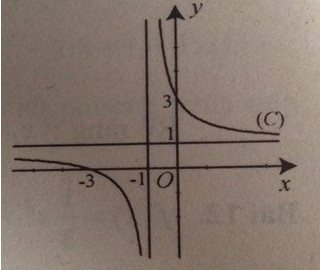
b) Xét phương trình có nghiệm là hoành độ giao điểm của (C) và đường thẳng (d): y = 2x + m
(1)
x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1
Δ = (m+1)2 – 4.2(m-3) = m2 – 6m + 25 = (m-3)2 + 16> 0, Δm, nên (1) luôn có hai nghiệm phân biệt khác -1.
Vậy (d) luôn cắt (C) tại hai điểm phân biệt M, N (hoành độ của M, N chính là nghiệm của (1)).
TenAnh1
C = (-4.24, -6.16)
C = (-4.24, -6.16)
C = (-4.24, -6.16)
D = (11.12, -6.16)
D = (11.12, -6.16)
D = (11.12, -6.16)
E = (-4.28, -6.08)
E = (-4.28, -6.08)
E = (-4.28, -6.08)
F = (11.08, -6.08)
F = (11.08, -6.08)
F = (11.08, -6.08)
Vậy \(Min_{MN}=2\sqrt{3}\) khi \(m=3\).

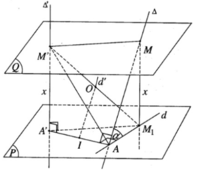
Hình tứ giác A’M’M M 1 là hình chữ nhật nên tâm O cũng là trung điểm của A’M. Do đó khi x thay đổi thì mặt phẳng (Q) thay đổi và điểm O luôn luôn thuộc đường thẳng d’ đi qua trung điểm I của đoạn AA’ và song song với đường thẳng ∆ . Vì mặt cầu tâm O luôn luôn đi qua hai điểm cố định A, A’nên nó có tâm O di động trên đường thẳng d’. Do đó mặt cầu tâm O luôn luôn chứa đường tròn tâm I cố định có đường kính AA’ cố định và nằm trong mặt phẳng cố định vuông góc với đường thẳng d’.

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

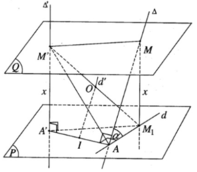
Vì mặt phẳng (P) qua A và vuông góc với Δ′ nên AA’ thuộc (P). Vì M thuộc ∆ mà d là hình chiếu vuông góc của ∆ trên (P) nên M 1 thuộc d. Vì MA ⊥ AA′ ⇒ M 1 A ⊥ AA′
Mặt khác M 1 A ⊥ M′A′ nên ta suy ra M 1 A ⊥ (AA′M′). Do đó M 1 A ⊥ M′A và điểm A thuộc mặt cầu đường kính M’ M 1
Ta có M′A′ ⊥ (P) nên M′A′ ⊥ A′ M 1 , ta suy ra điểm A’ cũng thuộc mặt cầu đường kính M’ M 1
Ta có (Q) // (P) nên ta suy ra
M M 1 ⊥ (Q) mà MM’ thuộc (Q), do đó M 1 M ⊥ MM′
Như vậy 5 điểm A, A’, M, M’, M 1 cùng thuộc mặt cầu (S) có đường kính M’ M 1 . Tâm O của mặt cầu (S) là trung điểm của đoạn M’ M 1
Ta có M ' M 1 2 = M ' A ' 2 + A ' M 1 2 = M ' A ' 2 + A ' A 2 + AM 1 2 = x 2 + a 2 + x 2 cot 2 α vì M M 1 = x
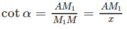
Bán kính r của mặt cầu (S) bằng (M′ M 1 )/2 nên