Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔDEF có \(EF^2=DE^2+DF^2\)
nên ΔDEF vuông tại D
b: Xét ΔDEF vuông tại D có DK là đường cao
nên \(\left\{{}\begin{matrix}DK\cdot FE=DE\cdot DF\\DF^2=FK\cdot FE\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DK=4.8\left(cm\right)\\FK=6.4\left(cm\right)\end{matrix}\right.\)


a, Ta có ∆DEF vuông vì D E 2 + D F 2 = F E 2
b, c, Tìm được: DK = 24 5 cm và HK = 32 5 cm
K D E ^ ≈ 36 0 52 ' ; K E D ^ = 35 0 8 '
d, Tìm được DM=3cm, FM=5cm và EM = 3 5 cm
e, f, Ta có: sin D F K ^ = D K D F ; sin D F E ^ = D E E F
=> D K D F = D E E F => ED.DF = DK.EF

a) Gọi O là trung điểm của AD
mà AD là đường kính
nên O là tâm của đường tròn đường kính AD
hay OA=OD=R
Ta có: ΔACD vuông tại C(AC⊥CD)
mà CO là đường trung tuyến ứng với cạnh huyền AD(O là trung điểm của AD)
nên \(CO=\dfrac{AD}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(OA=OD=\dfrac{AD}{2}\)(O là trung điểm của AD)
nên OC=OA=OD(1)
Ta có: ΔABC cân tại A(gt)
mà AH là đường cao ứng với cạnh đáy BC(gt)
nên AH là đường phân giác ứng với cạnh BC(Định lí tam giác cân)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)
hay \(\widehat{BAD}=\widehat{CAD}\)
Xét ΔABD và ΔACD có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(cmt)
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
⇒\(\widehat{ABD}=\widehat{ACD}\)(hai góc tương ứng)
mà \(\widehat{ACD}=90^0\)(AC⊥CD)
nên \(\widehat{ABD}=90^0\)
hay AB⊥BD
Ta có: ΔABD vuông tại B(AB⊥BD)
mà BO là đường trung tuyến ứng với cạnh huyền AD(O là trung điểm của AD)
nên \(BO=\dfrac{AD}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(AO=OD=\dfrac{AD}{2}\)(O là trung điểm của AD)
nên OB=OD=OA(2)
Từ (1) và (2) suy ra OB=OC=R
⇒B,C cùng thuộc đường tròn(O)
hay B,C cùng thuộc đường tròn đường kính AD(đpcm)

Tứ giác AEHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 o nên DE = AH.
Xét ABC vuông tại A có: A H 2 = HB.HC = 9.16 = 144 => AH = 12
Nên DE = 12cm
Đáp án cần chọn là: A

Tứ giác ARHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 ∘ nên DE = AH.
Xét ∆ ABC vuông tại A có A H 2 = HB.HC = 4.9 = 36 ⇔ AH = 6
Nên DE = 6cm
Đáp án cần chọn là : D

1: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{6}=\dfrac{CD}{8}\)
mà BD+CD=10cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{6}=\dfrac{CD}{8}=\dfrac{BD+CD}{6+8}=\dfrac{10}{14}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{30}{7}cm;CD=\dfrac{40}{7}cm\)

Theo định lý Pi-ta-go thì \(BC=\sqrt{5^2+12^2}=13\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác ta có:
\(BH=\frac{5^2}{13}=\frac{25}{13}\left(cm\right)\)
\(BH=\frac{12^2}{13}=\frac{144}{13}\left(cm\right)\)
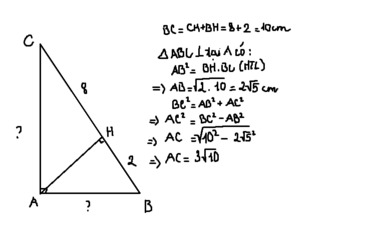
Áp dụng hệ thức lượng trong tam giác DEF vuông tại D có đường cao DM:
\(DM^2=EM.MF\Rightarrow DM=\sqrt{EM.MF}=\sqrt{2.8}=4\left(cm\right)\)
\(DE^2=EM.EF=2\left(2+8\right)=20\)
\(\Rightarrow DE=2\sqrt{5}\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}DM^2=ME\cdot MF=16\\DE^2=ME\cdot EF=2\left(2+8\right)=20\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}DM=4\left(cm\right)\\DE=2\sqrt{5}\left(cm\right)\end{matrix}\right.\)