Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu được sử dụng định lú Ptoleme thì bài này chứng minh rất đơn giản.
Không được sử dụng Ptoleme thì chúng ta dựng hình:
Dựng đường tròn tâm M bán kính MC cắt AM tại D \(\Rightarrow MC=MD\)
Mà \(\widehat{CMA}=\widehat{CBA}\) (cùng chắn cung AC) \(\Rightarrow\widehat{CMA}=60^0\)
\(\Rightarrow\Delta MCD\) đều \(\Rightarrow\widehat{MCD}=60^0\)
Lại có \(\left\{{}\begin{matrix}\widehat{ACD}+\widehat{DCB}=60^0\\\widehat{BCM}+\widehat{DCB}=60^0\end{matrix}\right.\) \(\Rightarrow\widehat{ACD}=\widehat{BCM}\)
Đồng thời \(AC=BC\) ; \(CD=CM\Rightarrow\Delta ACD=\Delta BCM\) (c.g.c)
\(\Rightarrow AD=BM\)
\(\Rightarrow AM=AD+DM=BM+CM\) (đpcm)


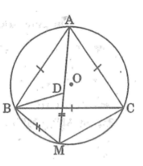
Ta có: ∆ ABD = ∆ CBM (cmt)
suy ra: AD = CM
Ta có: DM = BM ( tam giác MBD đều )
mà AM = AD + DM
suy ra: MA = MC + MB
Bạn tự vẽ hình nhé.
Lấy \(D\)thuộc \(AM\)sao cho \(MD=MB\)khi đó \(\Delta BMD\)là tam giác đều (tam giác cân có 1 góc bằng \(60^o\)là tam giác đều)
Ta có: \(\widehat{BAD}=\widehat{BCM}\)(1) (góc nội tiếp cùng chắn cung \(BM\))
\(\widehat{BDA}=180^o-\widehat{BDM}=180^o-60^o=120^o\)
\(\widehat{BMC}=180^o-\widehat{BAC}=180^o-60^o=120^o\)
Suy ra \(\widehat{BDA}=\widehat{BMC}\)(2)
Từ (1) và (2) suy ra \(\widehat{ABD}=\widehat{CBM}\).
Xét \(\Delta BDA\)và \(\Delta BMC\)có:
\(BA=BC\)(do \(ABC\)là tam giác đều)
\(\widehat{ABD}=\widehat{CBM}\)(cmt)
\(BM=BD\)(do \(\Delta BDM\)đều)
\(\Rightarrow\Delta BDA=\Delta BMC\)(c - g - c)
Suy ra \(DA=MC\)(hai cạnh tương ứng)
Vậy \(MA=MD+DA=MC+MB\)(đpcm).