Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Trên AM lấy điểm E sao cho ME = MB
Có : góc BME = góc BCA = 60 độ
=> tam giác EMB đều => EB = MB và góc EMB = 60 độ
Góc EMB = 60 độ => góc EBC + góc CBM = 60 độ
Lại có : góc ABC = 60 độ nên góc ABE + góc EBC = 60 độ
=> góc ABE = góc CBM
=> tam giác AEB = tam giác CMB (c.g.c)
=> AE = CM
=> AM = AE + EM = CM+BM
b, Theo câu a có tam giác AEB = tam giác CMB
=> góc EAB = góc MCB
=> tam giác MDC đồng dạng tam giác MBA (g.g)
=> MC/MA = MD/MB
=> MD.MA=MB.MC
Có : MD/MB + MD/MC = MD.(1/MB + 1/MC) = MD.(MB+MC)/MB.MC = MD/MA/MB.MC = 1

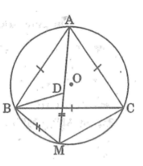
Ta có: ∆ ABD = ∆ CBM (cmt)
suy ra: AD = CM
Ta có: DM = BM ( tam giác MBD đều )
mà AM = AD + DM
suy ra: MA = MC + MB

A B C M D E
a) Xét \(\Delta MBD\)và \(\Delta MAC\)
có: \(\widehat{MAC}=\widehat{MBD}\)( cùng chắn cung MC)
\(\widehat{BMD}=\widehat{AMC}\)( cung AB=cung AC vì AB=AC)
=> \(\Delta MBD\)~ \(\Delta MAC\)
b) Từ câu a)_
=> \(\frac{MB}{MA}=\frac{BD}{AC}\)(1)
\(\frac{MC}{MA}=\frac{MD}{MB}\)(2)
Dễ dàng chứng minh đc:
\(\Delta BDM~\Delta ADC\)
=> \(\frac{MD}{MB}=\frac{DC}{AC}\)(3)
Từ (1), (2), (3)
=> \(\frac{MB}{MA}+\frac{MC}{MA}=\frac{BD}{AC}+\frac{CD}{AC}=\frac{BC}{AC}\)\(=\frac{BC}{AB}\)
c) Lấy điểm E thuộc đoạn