Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Em tự giải
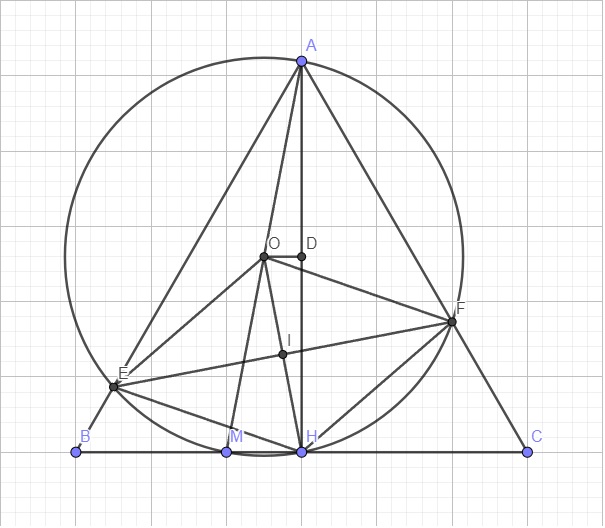
b. Do tam giác ABC đều và AH là đường cao \(\Rightarrow AH\) đồng thời là phân giác góc A
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}.60^0=30^0\)
AEMHF nội tiếp đường tròn tâm O \(\Rightarrow\widehat{HOF}=2.\widehat{CAH}=60^0\) (góc nội tiếp và góc ở tâm cùng chắn cung HF)
Mà \(OH=OF\) (cùng là bán kính) \(\Rightarrow\Delta OHF\) đều (tam giác cân có 1 góc 60 độ)
Tương tự ta có \(\widehat{HOE}=60^0\Rightarrow\Delta OHE\) đều
\(\Rightarrow OE=OF=HE=HF\Rightarrow OEHF\) là hình thoi
c.
Gọi D là trung điểm AH \(\Rightarrow OD\perp AH\) \(\Rightarrow OH\ge DH\Rightarrow OH\ge\dfrac{1}{2}AH\Rightarrow OH\ge\dfrac{a\sqrt{3}}{2}\)
Gọi I là giao điểm EF và OH \(\Rightarrow I\) là tâm hình thoi OEHF
\(S_{OEHF}=2S_{OHE}=2EI.OH=2\sqrt{OE^2-OI^2}.OH\)
\(=2OH.\sqrt{OH^2-\left(\dfrac{OH}{2}\right)^2}=OH^2\sqrt{3}\ge\left(\dfrac{a\sqrt{3}}{2}\right)^2.\sqrt{3}=\dfrac{3a^2\sqrt{3}}{2}\)
Dấu "=" xảy ra khi \(OH=DH\Leftrightarrow O\) trùng D
\(\Rightarrow M\) trùng H
hình bạn tự vẽ nha :
a.Ta có:
đường tròn đường kính
b.Từ câu a
Mà đều,
Do
đều
là hình thoi
a) Có nên 5 điểm A, P, M, H, Q cùng thuộc đường tròn đường kính AM.
b) Vì AH là đường cao của tam giác đều ABC nên .
Vì A, P, M, H, Q cùng nằm trên đường tròn tâm O nên OP = OH = OQ = OM và ; suy ra OPH và OQH là hai tam giác đều, do đó OQHP là hình thoi.
c) Gọi r là bán kính đường tròn ngoại tiếp đa giác APMHQ thì AM = 2r và OPH, OQH là hai tam giác đều cạnh r. Do đó
Do đó PQ ngắn nhất khi và chỉ khi M là trung điểm BC.
A) MP vuông góc AB tại P => góc MPA=90; MQ vuông góc AC tại Q=> MQA=90
=> tg APMQ nội tiếp(tổng 2 góc đối =90)
b) diện tích tam giác AMB=1/2.MP.AB=1/2.MP.BC; diện tích tam giác AMC=1/2.MQ.AC=1/2.MP.BC( AB=BC=CA tam giác đều)
S tam giác ABC=1/2.AH.BC
ta có: S AMB+S AMC=S ABC <=> \(\frac{1}{2}.MP.BC+\frac{1}{2}MQ.BC=\frac{1}{2}AH.BC\Leftrightarrow\frac{1}{2}BC\left(MP+MQ\right)=\frac{1}{2}.BC.AH\)
=> MP+MQ=AH
c) góc AHM=90(AH là đường cao)=> H cũng thuộc đường tròn đường kính AM <=> ngũ giác APMQH nội tiếp
(O): góc HAQ=1/2 góc HOQ(góc nt và góc ở tâm)
tam giác AHC vuông => góc HAC=90-C=90-60=30 độ hay HAQ=30(góc C=60 vì tam giác đều)
=> góc HOQ=2.30=60 .
(O): góc PAQ=1/2 góc POQ(góc nt và góc ở tâm) <=> góc POQ=2.60=120( góc PAQ hay BAC=60- tam giác đều)
góc HOQ=60 => OH là pg của góc POQ.
tam giác POQ có: OP=OQ=R=> tam giác cân => OH đồng thời là đường cao => OH vuông góc PQ