Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta\)ABC cân tại A có :
AH là đường cao
\(\Rightarrow\)AH là đường trung tuyến
\(\Rightarrow\)H là trung điểm của BC
\(\Rightarrow\)BH = HC =\(\dfrac{BC}{2}\)\(\dfrac{16}{2}=8\)
Xét \(\Delta\)AHB vuông tại H có:
\(\cos\)B=\(\dfrac{BH}{AB}=\dfrac{8}{10}\)=0.8
\(\Rightarrow\Lambda B\approx37\)độ
Ta có : góc B = góc C (Tam giác ABC cân tại A)
Mà góc B\(\approx37\)độ
\(\Rightarrow\)góc C\(\approx\)37 độ
b, Xét \(\Delta\)ABC có :
góc BAC+gócACB+góc ABC=180
\(\Rightarrow\)góc BAC=106 độ
Xét \(\Delta\)AHB vuông tại H có :
\(AB^2=AH^2+HB^2\Rightarrow AH=6\)
Ta có \(AI=\dfrac{1}{3}AH\Rightarrow HI=\dfrac{2}{3}AH\)
\(\Rightarrow\)HI=4cm
Xét tam giác BDC có
\(HI\) song song CD
\(\Rightarrow\dfrac{HI}{CD}=\dfrac{BH}{CH}=\dfrac{8}{16}=\dfrac{1}{2}\)
\(CD=8cm\)
Xét tứ giác AHCD có :
AH song somg CD
\(\Rightarrow\)AHCD là hình thang
Diện tích hình thang AHCD là :
\(\dfrac{1}{2}\left(6+8\right)\times8=56cm^2\)
Diện tích AHB là :
\(\dfrac{1}{2}\times6\times8=24cm^2\)
Diện tích tứ giác ABCD là
\(56+24=80cm^2\)

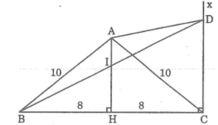
Áp dụng định lí Pi-ta-go vào tam giác vuông ABH ta có:
A B 2 = A H 2 + B H 2 ⇒ A H 2 = A B 2 - B H 2 = 10 2 - 8 2 = 36
Suy ra: AH = 6 (cm)
![]()
Suy ra: IH = AH – AI = 6 – 2 = 4 (cm)
Vì IH ⊥ BC và DC ⊥ BC nên IH // DC (1)
Mặt khác: BH = HC (gt) (2)
Từ (1) và (2) ta có IH là đường trung bình của tam giác BCD


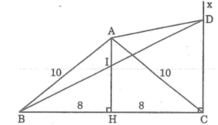
Ta có: AH ⊥ BC, suy ra: HB = HC = BC/2 = 8 (cm)
Trong tam giác vuông ABH, ta có:
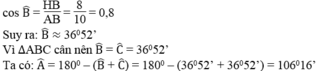


kẻ AK // BC
có AKCB là hình thang vuông KC = AH dễ dàng tính được
AK = HC và BC dễ dàng tính được vậy diện tích tứ giác AKCB tính được
bây h ta sẽ đi tính diện tích tam giác vuông AKD
có
[laTEX]\frac{IH}{DC} = \frac{BH}{BC} = \frac{1}{2} \Rightarrow DC = 2IH[/laTEX]
IH dễ dàng tính được nên DC tính được
KC = AH vậy KD = DC - KC cũng sẽ tính được
[laTEX]S_{AKD} = \frac{KD.KA}{2}[/laTEX]
có được 2 diện tích này rồi cộng vào là ra đáp án nhé ban

\(AB^2+AC^2=BC^2=25\Rightarrow5AC^2=25\Leftrightarrow AC=\sqrt{5}\left(cm\right)\Rightarrow AB=2\sqrt{5}\left(cm\right)\)\(CH=\dfrac{AC^2}{BC}=1\left(cm\right)\Rightarrow BH=5-1=4\left(cm\right)\\ AH=\dfrac{AB.AC}{BC}=2\\ AI=\dfrac{1}{3}AH=\dfrac{2}{3};HI=\dfrac{2}{3}AH=\dfrac{4}{3}\\ CD\text{//}AH\Rightarrow CD\text{//}HI\Rightarrow\dfrac{HI}{CD}=\dfrac{BH}{BC}=\dfrac{4}{5}\\ \Rightarrow CD=\dfrac{5}{4}HI=\dfrac{5}{4}\cdot\dfrac{4}{3}=\dfrac{5}{3}\\ \Rightarrow S_{AHCD}=\dfrac{1}{2}\cdot HC\cdot\left(AH+CD\right)=\dfrac{1}{2}\cdot1\cdot\left(2+\dfrac{5}{3}\right)=\dfrac{11}{6}\left(cm^2\right)\left(AH\text{//}CD\text{ nên }AHCD\text{ là hình thang}\right)\)
a) Tam giác ABC cân tại A có AH là đường cao nên H là trung điểm của BC.
Vì vậy BH = HC = 16 : 2 = 8(cm).
cos\widehat{ACB}=\dfrac{HC}{AC}=\dfrac{8}{10}=\dfrac{4}{5}cosACB=ACHC=108=54 suy ra \widehat{BCA}\cong36^o52'BCA≅36o52′.
Tam giác ABC cân tại A nên \widehat{ABC}=\widehat{ACB}=36^o52'ABC=ACB=36o52′.
\widehat{BAC}=180^o-\left(36^o52'+36^o52'\right)=106^o16'BAC=180o−(36o52′+36o52′)=106o16′.
b) Do CD//AH nên áp dụng định lý Ta-let ta có:
\dfrac{BH}{BC}=\dfrac{HI}{DC}=\dfrac{1}{2}BCBH=DCHI=21
Áp dụng định lý Pi-ta-go ta có:
AH=\sqrt{AC^2-HC^2}=6\left(cm\right)AH=AC2−HC2=6(cm).
Suy ra HI=\dfrac{2}{3}AH=4\left(cm\right)HI=32AH=4(cm).
Vì vậy DC=2HI=2.4=8\left(cm\right)DC=2HI=2.4=8(cm).
Diện tích tứ giác ABCD là:
S_{\Delta ABC}+S_{\Delta ADC}=\dfrac{1}{2}AH.BC+\dfrac{1}{2}HC.DCSΔABC+SΔADC=21AH.BC+21HC.DC =\dfrac{1}{2}.6.16+\dfrac{1}{2}.8.8=80\left(cm^2\right)=21.6.16+21.8.8=80(cm2)
a) Tam giác ABC cân tại A có AH là đường cao nên H là trung điểm của BC.
Vì vậy BH = HC = 16 : 2 = 8(cm).
cos\widehat{ACB}=\dfrac{HC}{AC}=\dfrac{8}{10}=\dfrac{4}{5}cosACB=ACHC=108=54 suy ra \widehat{BCA}\cong36^o52'BCA≅36o52′.
Tam giác ABC cân tại A nên \widehat{ABC}=\widehat{ACB}=36^o52'ABC=ACB=36o52′.
\widehat{BAC}=180^o-\left(36^o52'+36^o52'\right)=106^o16'BAC=180o−(36o52′+36o52′)=106o16′.
b) Do CD//AH nên áp dụng định lý Ta-let ta có:
\dfrac{BH}{BC}=\dfrac{HI}{DC}=\dfrac{1}{2}BCBH=DCHI=21
Áp dụng định lý Pi-ta-go ta có:
AH=\sqrt{AC^2-HC^2}=6\left(cm\right)AH=AC2−HC2=6(cm).
Suy ra HI=\dfrac{2}{3}AH=4\left(cm\right)HI=32AH=4(cm).
Vì vậy DC=2HI=2.4=8\left(cm\right)DC=2HI=2.4=8(cm).
Diện tích tứ giác ABCD là:
S_{\Delta ABC}+S_{\Delta ADC}=\dfrac{1}{2}AH.BC+\dfrac{1}{2}HC.DCSΔABC+SΔADC=21AH.BC+21HC.DC =\dfrac{1}{2}.6.16+\dfrac{1}{2}.8.8=80\left(cm^2\right)=21.6.16+21.8.8=80(cm2).