Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác HAD và tam giác HCB có:
+ HD = HB (gt).
+ \(\widehat{AHD}=\widehat{CHB}\) (đối đỉnh).
+ HA = HC (H là trung điểm AC).
=> Tam giác HAD = Tam giác HCB (c - g - c).
b) Xét tứ giác ADCB có:
+ H là trung điểm AC (gt).
+ H là trung điểm BD (HD = HB).
=> Tứ giác ADCB là hình bình hành (dhnb).
=> AB // DC (Tính chất hình bình hành).
c) Ta có: AB // DC (cmt). \(\Rightarrow\widehat{HAM}=\widehat{HCN}\) (SLT).
Xét tam giác AHM và tam giác CHN có:
+ \(\widehat{AHM}=\widehat{CHN}\) (đối đỉnh).
+ AH = CH (H là trung điểm AC).
+ \(\widehat{HAM}=\widehat{HCN}\) (cmt).
=> Tam giác AHM = Tam giác CHN (g - c - g).
Xét tam giác CMH và tam giác ANH có:
+ CH = AH (Tam giác AHM = Tam giác CHN).
+ \(\widehat{CHM}=\widehat{AHN}\) (đối đỉnh).
+ MH = NH (Tam giác AHM = Tam giác CHN).
=> Tam giác CMH = Tam giác ANH (c - g - c).

a) Xét tam giác AHB và tam giác AHE có
BH=HE
AH chung
góc AHE= góc AHB= 90 độ ( AH vuông góc với BC)
=> tam giác AHB= tam giác AHE (c.g.c)
=>HE=HB
b) Xét tam giác AHB và tam giác DHE có
góc DHE = góc AHB ( đối đỉnh)
HE=HB (cmt)
AH=HD
=> tam giác AHB=tam giác DHE (c.g.c)
=> DE= AB ( 2 cạnh tương ứng)
=> tam giác DHE= tam giác AHE =tam giác AHB
=> AE=DE(2 cạnh tương ứng)
c) Xét tam giác AHC và tam giác DHC có
HC chung
góc AHE=góc DHE=90 độ
AH=HD
=> tam giác AHC= tam giác DHC( cạnh huyền-góc nhọn)
=>AC=DC (2 cạnh tương ứng)
Xét tam giác ACE và tam giác DCE có
AE= DE (cmt)
AC= DC(cmt)
CE chung
=> tam giác ACE= tam giác DCE(c.c.c)
=> góc EAC= góc EDC (2 góc tương ứng)
d)Ta có: C,E,B thẳng hàng
=> góc CEA+ góc AEB= 180 độ
Mà góc CEN và góc AEB là 2 góc đối đỉnh
=>góc AEC+ góc CEN= 180 độ
=> A,E,N thẳng hàng

a: Xét ΔABM và ΔCDM có
MA=MC
góc AMB=góc CMD
MB=MD
Do đó: ΔABM=ΔCDM
b: ΔABM=ΔCDM
nên AB=CD và góc ABM=góc CDM
=>AB//CD
=>CE vuông góc với AC
=>AC vuông góc DE

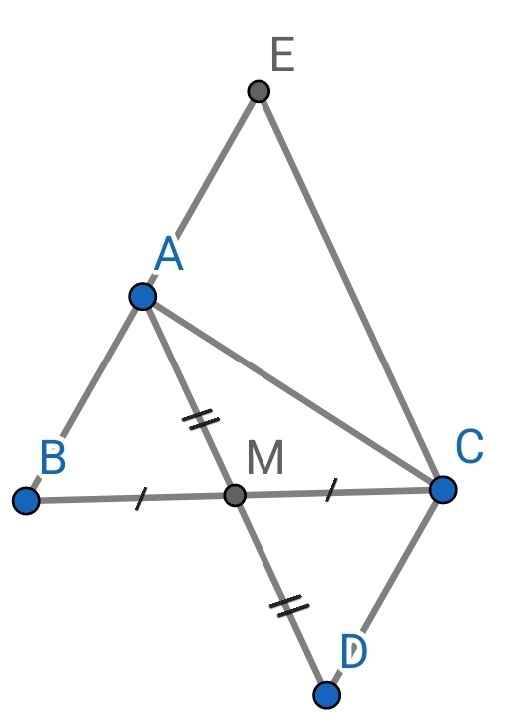 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE

(Bạn tự vẽ hình giùm)
a/ \(\Delta ADM\)và \(\Delta CBM\)có: AM = CM (M là trung điểm của AC)
\(\widehat{AMD}=\widehat{BMC}\)(đối đỉnh)
DM = BM (gt)
=> \(\Delta ADM\)= \(\Delta CBM\)(c. g. c) => AD = BC (hai cạnh tương ứng)
b/ \(\Delta ABM\)và \(\Delta CDM\)có: AM = CM (M là trung điểm của AC)
\(\widehat{AMB}=\widehat{CMD}\)(đối đỉnh)
BM = DM (gt)
=> \(\Delta ABM\)= \(\Delta CDM\)(c. g. c)
=> \(\widehat{BAM}=\widehat{MCD}=90^o\)(hai góc tương ứng)
=> AC _|_ CD (đpcm)
a) *Xét \(\Delta HAD\) và \(\Delta HCB\) có:
\(\left\{{}\begin{matrix}AH=HC\left(gt\right)\\\widehat{AH\text{D}}=\widehat{CHB}\left(\text{đ}\text{ối}.\text{đ}\text{ỉnh}\right)\\BH=HD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta HAD=\Delta HCB\left(c-g-c\right)\)
b) *Xét \(\Delta AHB\) và \(\Delta CHD\) có:
\(\left\{{}\begin{matrix}AH=HC\left(gt\right)\\\widehat{AHB}=\widehat{CHD}\left(\text{đ}\text{ối}.\text{đ}\text{ỉnh}\right)\\BH=HD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AHB=\Delta CHD\left(c-g-c\right)\)
\(\Rightarrow\widehat{HAB}=\widehat{HCD}\) (hai góc tương ứng)
Mà \(\widehat{HAB}\) và \(\widehat{HCD}\) ở vị trí so le trong
\(\Rightarrow AB//CD\)
c) *Xét \(\Delta AHM\) và \(\Delta CHN\)có:
\(\left\{{}\begin{matrix}AH=HC\left(gt\right)\\\widehat{AHM}=\widehat{CHN}\left(\text{đ}\text{ối}.\text{đ}\text{ỉnh}\right)\\\widehat{HAM}=\widehat{HCN}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AHM=\Delta CHN\left(g-c-g\right)\)
\(\Rightarrow MH=HN\) (hai cạnh tương ứng)
*Xét \(\Delta CMH\) và \(\Delta ANH\) có:
\(\left\{{}\begin{matrix}CH=AH\left(gt\right)\\\widehat{MHC}=\widehat{NHA}\left(\text{đ}\text{ối}.\text{đ}\text{ỉnh}\right)\\MH=HN\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta CMH=\Delta ANH\left(c-g-c\right)\)
ĐÚNG