Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

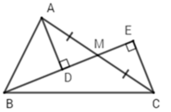
Xét tam giác ADM và tam giác CEM có:
ADM = CEM (= 90 độ)
AM = MC (M là trung điểm của AC)
AMD = CME (đối đỉnh)
=> tam giác ADM = tam giác CEM
=> DM = EM (2 cạnh tương ứng)
=> M là trung điểm của DE
b) ta có:
BD + BE = BD + BD + DE
mà ED = DM+EM và DM = EM
=> BD + BE = 2BD + 2DM = 2BM
trong tam giác ABM có A là góc vuông
=> AB^2 + AM^2 = BM^2 (định lí Pytago)
=> AB<BM
=> 2AB < 2BM
=> 2AB < BD+BE

a: Xét ΔAHB và ΔCKA có
góc AHB=góc AKC=90 độ
AB=CA
góc HAB=góc ACK
=>ΔAHB=ΔCKA
b: ΔAHB=ΔCKA
=>AH=CK
Xet ΔHIA và ΔKIC có
IA=IC
AH=CK
góc HAI=góc ICK
=>ΔHIA=ΔKIC
=>IH=IK
c: \(S_{BCKH}=\dfrac{1}{2}\cdot\left(BH+CK\right)\cdot HK\)
\(=\dfrac{1}{2}\cdot HK^2=IM^2< =IA^2\)
Dấu = xảy ra khi M trùng với A
=>d vuông góc AI