Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: cos B=3/5 nên sin B=4/5
=>AC/BC=4/5
=>AC=8cm
=>AB=6cm
\(HC=\dfrac{8^2}{10}=6.4\left(cm\right)\)
\(M=\left(2\cdot\dfrac{3}{5}-3\cdot\dfrac{4}{5}\right):\left(1+\dfrac{4}{5}:\dfrac{3}{5}\right)\)
\(=\dfrac{-6}{5}:\left(1+\dfrac{4}{3}\right)=\dfrac{-6}{5}:\dfrac{7}{3}=\dfrac{-6}{5}\cdot\dfrac{3}{7}=\dfrac{-18}{35}\)
b: \(AD=\dfrac{AC^2}{AH}=\dfrac{8^2}{4.8}=\dfrac{40}{3}\left(cm\right)\)
\(CD=\sqrt{\left(\dfrac{40}{3}\right)^2-8^2}=\dfrac{32}{3}\left(cm\right)\)
c: \(AE\cdot EB+AF\cdot FC\)
=HE^2+HF^2
=EF^2
=AH^2

Bài 1:
B A C H D
\(BC=CD+BD=68+51=119\)
\(AD\)là phân giác \(\widehat{BAC}\)\(\Rightarrow\)\(\frac{BD}{AB}=\frac{DC}{AC}\)hay \(\frac{51}{AB}=\frac{68}{AC}\)
\(\Leftrightarrow\)\(\frac{51^2}{AB^2}=\frac{68^2}{AC^2}=\frac{51^2+68^2}{AB^2+AC^2}=\frac{25}{49}\)
suy ra: \(\frac{51^2}{AB^2}=\frac{25}{49}\)\(\Rightarrow\)\(AB=71,4\)
ÁP dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Leftrightarrow\)\(BH=\frac{AB^2}{BC}=\frac{71,4^2}{119}=42,84\)
\(\Rightarrow\)\(CH=BC-BH=119-42,84=76,16\)
Bài 2:
B A C H
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Leftrightarrow\)\(BH^2=AB^2-AH^2\)
\(\Leftrightarrow\)\(BH^2=7,5^2-6^2=20,25\)
\(\Leftrightarrow\)\(BH=4,5\)
Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}=\frac{7,5^2}{4,5}=12,5\)
\(AB.AC=BC.AH\)
\(\Rightarrow\)\(AC=\frac{BC.AH}{AB}=\frac{12,5.6}{7,5}=10\)
b) \(cosB=\frac{AC}{BC}=\frac{10}{12,5}=0.8\)
\(cosC=\frac{AB}{BC}=\frac{7,5}{12,5}=0,6\)

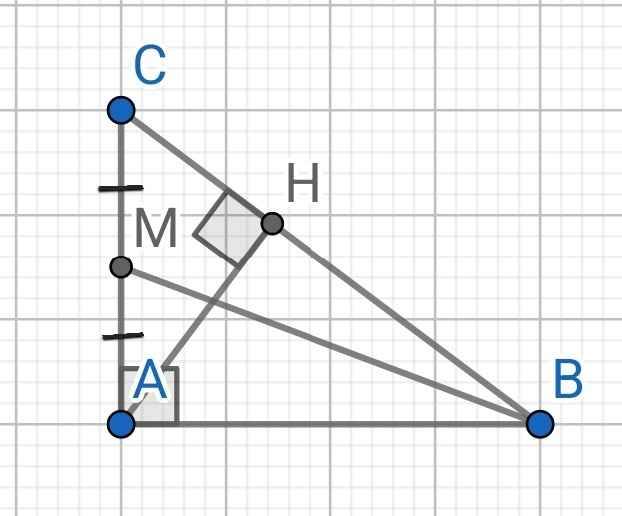
\(tanB=\dfrac{AC}{AB}=\dfrac{5}{12}\)
⇒ AC = \(\dfrac{5}{12}\) .AB
= \(\dfrac{5}{12}.5\)
\(=\dfrac{25}{12}\) (cm)
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
\(=5^2+\left(\dfrac{25}{12}\right)^2\)
= \(\dfrac{4225}{144}\)
⇒ BC = \(\dfrac{65}{12}\) (cm)
AH.BC = AB.AC
⇒ AH = AB . AC : BC
= 5 . \(\dfrac{25}{12}:\dfrac{65}{12}\)
\(=\dfrac{25}{13}\left(cm\right)\)
M là trung điểm của AC
⇒ AM = AC : 2 = \(\dfrac{25}{12}:2\) \(=\dfrac{25}{24}\) (cm)
∆ABM vuông tại A
⇒ BM² = AB² + AM²
= \(5^2+\left(\dfrac{25}{24}\right)^2\)
= \(\dfrac{15025}{576}\)
⇒ BM = \(\dfrac{5\sqrt{601}}{24}\) (cm)

1
\(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{.4}AC\)
Theo pytago xét tam giác ABC vuông tại A có:
\(\sqrt{AB^2+AC^2}=BC^2\\ \Rightarrow\sqrt{\left(\dfrac{3}{4}AC\right)^2+AC^2}=10\\ \Rightarrow AC=8\\ \Rightarrow AB=\dfrac{3.8}{4}=6\)
Theo hệ thức lượng xét tam giác ABC vuông tại A, đường cao AH có:
\(AB^2=BH.BC\\ \Leftrightarrow BH=\dfrac{AH^2}{BC}=\dfrac{6^2}{10}=3,6\)
2
\(\dfrac{AB}{AC}=\dfrac{27}{4}\Rightarrow AB=\dfrac{27}{4}AC\)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{27}{4}AC\right)^2+AC^2}=\dfrac{\sqrt{745}AC}{4}\) ( Theo pytago trong tam giác ABC vuông tại A)
Theo hệ thức lượng trong tam giác ABC vuông tại A, đường cao AH có:
\(AH.BC=AB.AC\\ \Leftrightarrow33,6.\dfrac{\sqrt{745}}{4}AC=\dfrac{27}{4}AC.AC\\ \Rightarrow AC=\dfrac{56\sqrt{745}}{45}\)
\(\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{27}{4}.\dfrac{56\sqrt{745}}{45}=\dfrac{42\sqrt{745}}{5}\\BC=\dfrac{\sqrt{745}}{4}.\dfrac{56\sqrt{745}}{45}=\dfrac{2086}{9}\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}AC\approx33,97\\AB\approx229,28\\BC\approx231,78\end{matrix}\right.\)
3
`BC=HB+HC=36+64=100`
Theo hệ thức lượng có (trong tam giác ABC vuông tại A đường cao AH):
\(AH^2=HB.HC\\ \Rightarrow AH=\sqrt{36.64}=48\)
\(AB=\sqrt{HB.BC}=\sqrt{36.100}=60\\ AC=\sqrt{HC.BC}=\sqrt{64.100}=80\)

Pytago ra BC=35
Áp dụng hệ thức lượng ra:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{441}+\frac{1}{784}\Rightarrow AH=\frac{84}{5}\)
AB2=HB.BC→HB=441:35=12.6
HC=BC-HB=35-12.6=22.4
b, Tính theo ct thôi vì biết các cạnh rồi.
c,Theo t/c đường phân giác có
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{3}{4}\Rightarrow\frac{BD}{CD}=\frac{3}{4}\Rightarrow\frac{BD+CD}{CD}=\frac{3+4}{4}\Rightarrow\frac{BC}{CD}=\frac{7}{4}\Rightarrow CD=20;BD=15\)

Xét △ABC vuông tại A có:
\(\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{3}{4}\Rightarrow AC=\dfrac{3}{4}AB\)
Lại có: \(AB^2+AC^2=BC^2=10^2=100\)
\(\Rightarrow AB^2+\left(\dfrac{3}{4}AB\right)^2=100\)
\(\Rightarrow\dfrac{25}{16}AB^2=100\Rightarrow AB^2=64\Rightarrow AB=8\left(cm\right)\)
\(\Rightarrow AC=\dfrac{3}{4}AB=\dfrac{3}{4}.8=6\left(cm\right)\)
\(P_{ABC}=AB+BC+CA=6+10+8=24\left(cm\right)\)
