
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

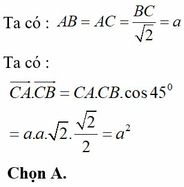


a) \(BC.AH=AB.AC=6.8=48cm^2\) (bằng 2 lần diện tích ABC).
b) HAB và HAC là 2 tam giác vuông có \(\stackrel\frown{HBA}=\widehat{HAC}\) (cùng phụ với \(\widehat{BCA}\)) nên HAB đồng dạng với HAC. Từ đó \(\dfrac{HB}{AH}=\dfrac{AH}{HC}\Rightarrow HB.HC=AH^2\) (đây là hệ thức lượng quen thuộc trong tam giác vuông: đường cao thuộc cạnh huyền bằng trung bình nhân của hai cạnh góc vuông)
c) Áp dụng Pitago ta có \(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10cm\). Từ đó \(BE=BCV-CE=10-4=6cm=BA\).
Ta có \(BE^2=BA^2=BH.BC\) (chứ không phải là \(BH.CH\) nhé).
d) Không biết là bạn cần tính gì? Nếu là cần tính diện tích của tam giác CED thì có thể làm như sau:
Áp dụng tính chất phân giác có \(\dfrac{CD}{AD}=\dfrac{BC}{BA}=\dfrac{10}{6}=\dfrac{5}{3}\Rightarrow\dfrac{CD}{CA}=\dfrac{CD}{CD+AD}=\dfrac{5}{3+5}=\dfrac{5}{8}\)
\(\dfrac{dt_{CED}}{dt_{CAB}}=\dfrac{CE}{CB}.\dfrac{CD}{CA}=\dfrac{4}{10}.\dfrac{5}{8}=\dfrac{1}{4}\), do đó \(dt_{CED}=\dfrac{1}{4}dt_{ABC}=\dfrac{1}{4}.\dfrac{1}{2}.6.8=6cm^2\)
Tại sao (diện tích tam giác ced / diện tích tam giác cab) =ce/cb*cd/ca

a) Do A + B + C = 180 độ nên góc A bù với góc B + C => sin(B + C) = sinA (sin hai góc bù bằng nhau)
(A + B)/2 + C/2 = 90 độ => hai góc (A + B)/2 và C/2 là hai góc phụ nhau => cos (A + B)/2 = sin(C/2) (Chắc đề bài bạn cho nhầm thành sinC)
b) Bạn xem lại đề nhé
c) \(sin^6a+cos^6a+3sin^2a.cos^2a=\left(sin^2a\right)^3+\left(cos^2a\right)^3+3.sin^2a.cos^2a\)
= \(\left(sin^2a+cos^2a\right)\left(sin^4a+cos^4a-sin^2a.cos^2a\right)+3sin^2a.cos^2a\)
= \(sin^4a+cos^4a+2sin^2a.cos^2a\)
= \(\left(sin^2a+cos^2a\right)^2=1\)

Ta có tam giác vuông ABH = CAI (c.h-g.n) => BH = AI
Áp dụng Pytago trong tam giác vuông ACI có:
AC² = AI² + IC² hay AC² = BH² + IC²
Đặt AB = AC = a; áp dụng Pytago trong tam giác vuông ABC ta có BC² = 2a²
Vậy BC²/( BH² + CI²) = BC²/ AC² = 2a²/a² = 2

a: Xét ΔADE có
AB/BD=AC/CE
nên DE//BC
b: Xét ΔDBM vuông tại M và ΔECN vuông tại N có
DB=EC
\(\widehat{DBM}=\widehat{ECN}\)
Do đó: ΔDBM=ΔECN
Suy ra: BM=CN
c: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
DO đó: ΔABM=ΔACN
Suy ra: AM=AN
hay ΔAMN cân tại A

a: Ta có: ΔABC cân tại A
mà AI là đường phân giác
nên AI là đường cao
b: Ta có: ΔABC cân tại A
mà AI là đường cao
nên I là trung điểm của BC
Xét ΔABC có
AI là đường trung tuyến
BD là đường trung tuyến
AI cắt BD tại M
Do đó: M là trọng tâm của ΔABC
c: BM=CM=BC/2=3(cm)
Xét ΔABM vuông tại M có
\(AB^2=AM^2+MB^2\)
hay AM=4(cm)

Sửa lại đề nha
Cho tam giác ABC cân tại A
A B C D E I
a) Vì \(\Delta ABC\)cân tại A
=> B = C và AB = AC
Vì \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
\(\widehat{AED}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ ( 1 ) và ( 2 ) => \(\widehat{ABD}=\widehat{AED}\)
mà hai góc này ở vị trí đồng vị
=> ED // BC
mà \(\widehat{ABC}=\widehat{ACB}\)( \(\Delta ABC\)cân A )
=> Tứ giác BEDC là hình thang cân
b)
Vì ED // BC
=> \(\widehat{DEC}=\widehat{ECB}\)
mà góc \(\widehat{ECD}=\widehat{DCE}\)( CE là phân giác )
=> \(\widehat{DEC}=\widehat{DCE}\)
=> \(\Delta EDC\)cân
=> ED = DC
mà BE = DC ( tứ giác BEDC là hình thang cân )
=> BE = ED = DC
c )
Vì BD là phân giác của góc B
CE là phân giác của góc C
Mà BD giao CE tại I
=> I là trọng tâm \(\Delta ABC\)
=> AI là là đường trung trực
mà \(\Delta ABC\)cân A
=> AI là đường trung trực , phân giác ,trung tuyến đồng thời là đường cao
=> Ai là trung trực của DE và BC
d)
Vì \(\Delta ABC\)cân tại A
Mà góc A = 500
=> B = C = 650
=> DEB = EDC = 1150
Study well
Bạn Tham khảo nha
À chết
Phần a
chỗ từ ( 1 ) và ( 2 ) =>
thì phải là
\(\widehat{ABC}=\widehat{AED}\)nha mk làm nhầm sorry