Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa câu b: Từ M kẻ ME
Bg
a/ Xét hai tam giác AMB và AMC có:
AB = AC (gt)
BM = MC (vì M là trung điểm của BC)
AM là cạnh chung
Nên \(\Delta AMB=\Delta AMC\)(c.c.c)
Vậy \(\Delta AMB=\Delta AMC\)
b/ Xét hai tam giác vuông AME và AMF có:
\(\widehat{EAM}=\widehat{FAM}\)(vì \(\Delta AMB=\Delta AMC\))
AM là cạnh chung
Nên \(\Delta AME=\Delta AMF\)(g.c.g)
Do đó AE = AF (hai cạnh tương ứng)
Vậy AE = AF
c và d hơi dài. Đợi một thời gian :((

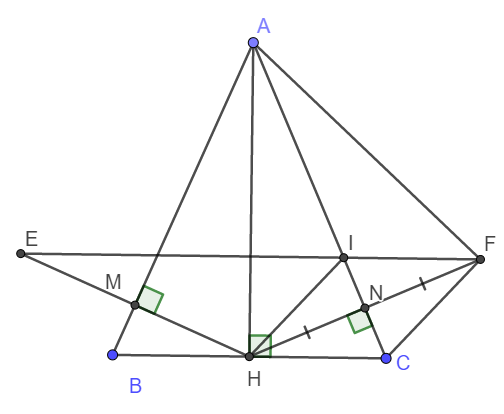
a) Do ABC là tam giác cân tại A nên AH là đường cao hay đồng thời là đường phân giác.
Xét tam giác vuông AMH và tam giác vuông ANH có:
Cạnh AH chung
\(\widehat{MAH}=\widehat{NAH}\)
\(\Rightarrow\Delta AMH=\Delta ANH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HM=HN.\)
b) Dễ dàng thấy ngay AC là đường trung trực của HF.
Khi đó thì AH = AF; CH = CF
Xét tam giác AHC và tam giác AFC có:
Cạnh AC chung
AH - AF
CH = CF
\(\Rightarrow\Delta AHC=\Delta AFC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFC}=\widehat{AHC}=90^o\Rightarrow AF\perp CF.\)
c) Ta thấy ngay \(\Delta HIN=\Delta FCN\left(g-c-g\right)\)
\(\Rightarrow IN=CN\)
Xét tam giác vuông INF và tam giác vuông CNH có:
HN = FN
IN = CN
\(\Rightarrow\Delta INF=\Delta CNH\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{IFN}=\widehat{CHN}\)
Mà chúng lại ở vị trí so le trong nên IF // BC.
d) Chứng minh tương tự câu c, ta có IE // BC
Vậy thì qua I có hai tia IE và IF cùng song song với BC nên chúng trùng nhau.
Vậy I, E, F thẳng hàng.

a) Xét tứ giác AEMF có
\(\widehat{EAF}=90^0\)(gt)
\(\widehat{AEM}=90^0\)(gt)
\(\widehat{AFM}=90^0\)(gt)
Do đó: AEMF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Xét ΔABC có
M là trung điểm của BC(gt)
MF//AB(cùng vuông góc với AC)
Do đó: F là trung điểm của AC(Định lí 1 về đường trung bình của tam giác)
Xét ΔABC có
M là trung điểm của BC(gt)
F là trung điểm của AC(cmt)
Do đó: MF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: \(MF=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà AE=MF(AFME là hình chữ nhật)
nên \(AE=\dfrac{AB}{2}\)
mà A,E,B thẳng hàng(gt)
nên E là trung điểm của AB
Ta có: F là trung điểm của NM(gt)
nên \(MN=2\cdot MF\)(1)
Ta có: E là trung điểm của AB(cmt)
nên AB=2AE(2)
Ta có: AEMF là hình chữ nhật(cmt)
nên MF=AE(Hai cạnh đối)(3)
Từ (1), (2) và (3) suy ra MN=AB
Xét tứ giác ABMN có
MN//AB(cùng vuông góc với AC)
MN=AB(cmt)
Do đó: ABMN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
