
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) \(B\subset A\)
\(\Rightarrow\left(-4;5\right)\subset\left(2m-1;m+3\right)\)
\(\Rightarrow2m-1\le-4< 5\le m+3\)
\(\Rightarrow\hept{\begin{cases}2m-1\ge4\\5\le m+3\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}m< -\frac{3}{2}\\m\ge2\end{cases}}\left(ktm\right)\)
\(\Rightarrow m\in\varnothing\)
b) \(A\text{∩ }B=\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m+3< -4\\5< 2m-1\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}m< -7\\m>3\end{cases}}\)
Vậy \(m< -7;m>3\)

thích làm mỗi bài 10:
\(\left\{\begin{matrix}x+y=45\\8x+9y=379\end{matrix}\right.\)
số hs dc điểm x = 26hs
x = 26 hs9đ


Lời giải:
Ta có:
\(5\overrightarrow{SA}-2\overrightarrow{SB}-\overrightarrow{SC}=\overrightarrow{0}\)
\(\Leftrightarrow 2\overrightarrow{SA}+2(\overrightarrow{SA}-\overrightarrow{SB})+(\overrightarrow{SA}-\overrightarrow{SC})=\overrightarrow{0}\)
\(\Leftrightarrow 2\overrightarrow{SA}+2\overrightarrow{BA}+\overrightarrow{CA}=\overrightarrow{0}\)
\(\Leftrightarrow 2(\overrightarrow {AS}+\overrightarrow{AB})+\overrightarrow{AC}=\overrightarrow{0}\)
Như vậy, ta có thể xác định điểm $S$ như sau:
Trên tia đối của tia $AC$ lấy điểm $R$ sao cho \(AR=\frac{AC}{2}\)
Khi đó, \(\overrightarrow{AC},\overrightarrow{AR}\) là các tia ngược hướng nhau nên \(\overrightarrow{AC}+2\overrightarrow{AR}=\overrightarrow{0}\)
Lấy điểm $S$ thỏa mãn \(ASRB\) là hình bình hành, khi đó, theo tính chất hình bình hành thì \(\overrightarrow{AB}+\overrightarrow{AS}=\overrightarrow{AR}\)
Như vậy, \(2(\overrightarrow{AS}+\overrightarrow{AB})+\overrightarrow{AC}=2\overrightarrow{AR}+\overrightarrow{AC}=\overrightarrow{0}\) , thỏa mãn đktđb
Vậy điểm $S$ xác định như trên là điểm cần tìm.
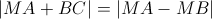


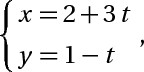
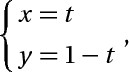
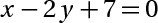
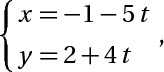 d2:
d2: 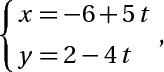
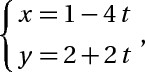 d2 : 2x+4y-10=0
d2 : 2x+4y-10=0 


Lời giải:
Lấy điểm $K$ sao cho $AKCB$ là hình bình hành
Khi đó: \(\overrightarrow{AK}=\overrightarrow {BC}\Leftrightarrow \overrightarrow{KA}+\overrightarrow{BC}=\overrightarrow{0}\)
Ta có:
\(|\overrightarrow{MA}+\overrightarrow{BC}|=|\overrightarrow{MA}-\overrightarrow{MB}|\)
\(\Leftrightarrow |\overrightarrow{MK}+\overrightarrow{KA}+\overrightarrow{BC}|=|\overrightarrow {BA}|\)
\(\Leftrightarrow |\overrightarrow{MK}|=|\overrightarrow{BA}|\)
Vậy tập hợp điểm M nằm trên đường tròn tâm $M$ bán kính \(R=AB\)