Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Bởi vì CM trực tiếp hơi khó nên mình CM bằng trùng hình)
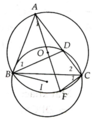
Vẽ \(AM\) là trung tuyến của tam giác \(ABC\) và tia \(AE\) thoả \(\widehat{BAE}=\widehat{CAM}\) (trong đó \(E\in\left(O\right)\)). Gọi \(D',N\) lần lượt là trung điểm của \(AE,AC\).
-----
Bước 1: CM: \(\widehat{AD'O}=90^o\) (hiển nhiên).
Bước 2: CM \(D\) trùng với \(D'\).
Tam giác \(ABE\) và \(AMC\) đồng dạng (g.g) nên tam giác phân bởi đường trung tuyến cũng đồng dạng.
Cụ thể là tam giác \(ABD'\) và \(AMN\) đồng dạng.
Suy ra \(\widehat{ABD'}=\widehat{AMN}=\widehat{BAM}\) (so le trong, \(MN\) song song \(AB\)).
Mà \(\widehat{BAM}=\widehat{EAC}\) nên \(\widehat{ABD'}=\widehat{D'AC}\).
Từ đó suy ra \(AC\) tiếp xúc với đường tròn ngoại tiếp \(ABD'\).
Tương tự suy ra \(AB\) tiếp xúc với đường tròn ngoại tiếp \(ACD'\).
Vậy \(D\) trùng với \(D'\) và ta có đpcm.

Ta có ; \(\widehat{A_1}=\widehat{A_2}\left(gt\right)\)
=> D là điểm chính giữa cung BC
=> DO vuông góc với BC tại trung điểm H của BC
lại có: \(\Delta BDM~\Delta BCF\Rightarrow\frac{BD}{BC}=\frac{DM}{CF}\Rightarrow\frac{BD}{2BH}=\frac{\frac{1}{2}DA}{CF}\Rightarrow\frac{BD}{BH}=\frac{DA}{CF}\)
Mà \(\widehat{D_1}=\widehat{C_2}\)( bẹn chứng minh ở phần a nhé)
\(\Rightarrow\Delta BDA~\Delta HCF\left(c.g.c\right)\Rightarrow\widehat{F_1}=\widehat{A_1}\)(2 góc tương ứng)
Mà A1=A2(gt) và A2=E1(cùng chắn 1 cung DC).
F1=E1=> tam giác EFHC nội tiếp