Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Xét tứ giác BEHF có: góc BFH + góc BEH = 900 + 900 = 1800
=> Tứ giác BEHF nội tiếp.
b, Xét tứ giác AFEC có :
góc AFC = góc AEC ( = 900) (Hai góc cùng nhìn 1 cạnh dưới 1 góc vuông)
=> Tứ giác AFEC nội tiếp
a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc DFC=góc EBC
góc EFC=góc DAC
góc EBC=góc DAC
=>góc DFC=góc EFC
Giải chi tiết:
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Ta có ∠AEH=∠AFH=90o⇒∠AEH=∠AFH=90o⇒ E, F thuộc đường tròn đường kính AH
⇒⇒ A, E, H, F cùng thuộc một đường tròn
⇒AEHF⇒AEHF là tứ giác nội tiếp (dhnb).
Ta có ∠BEC=∠BFC=90o⇒∠BEC=∠BFC=90o⇒ BCEF là tứ giác nội tiếp (dhnb)
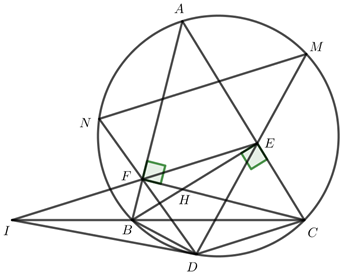
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (O)(O)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh ID2=IB.ICID2=IB.IC.
Xét ΔIBDΔIBD và ΔIDCΔIDC có:
∠I∠I chung
∠IDB=∠ICD∠IDB=∠ICD (ID là tiếp tuyến của (O)(O))
⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).
c) DE, DF cắt đường tròn (O)(O) tại M và N. Chứng minh NM // EF.
Xét ΔIBEΔIBE và ΔIFCΔIFC có:
∠I∠I chung
∠IEB=∠ICF∠IEB=∠ICF (BCEF là tứ giác nội tiếp)
⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF (kết hợp b)
⇒ID2=IE.IF⇒IDIE=IFID⇒ID2=IE.IF⇒IDIE=IFID
Xét ΔIDFΔIDF và ΔIEDΔIED có:
∠I∠I chung
IDIE=IFID(cmt)IDIE=IFID(cmt)
⇒ΔIDF∼ΔIED⇒∠IDF=∠IED⇒ΔIDF∼ΔIED⇒∠IDF=∠IED (2 góc tương ứng)
Mặt khác ∠IDF=∠NMD∠IDF=∠NMD (ID là tiếp tuyến của (O)(O)) ⇒∠IED=∠NMD⇒∠IED=∠NMD (tc)
Mà hai góc này ở vị trí đồng vị ⇒⇒ NM // EF.
a) Ta có: \(\angle AMH=\angle AEH=90\Rightarrow AEMH\) nội tiếp
\(\Rightarrow\angle AME=\angle AHE\)
Ta có: \(\angle HEC+\angle HDC=90+90=180\Rightarrow HECD\) nội tiếp
\(\Rightarrow\angle AHE=\angle ACD\Rightarrow\angle AME=\angle ACD\Rightarrow MECI\) nội tiếp
\(\Rightarrow\angle AME=\angle ACI\)
Xét \(\Delta AME\) và \(\Delta ACI:\) Ta có: \(\left\{{}\begin{matrix}\angle AME=\angle ACI\\\angle CAIchung\end{matrix}\right.\)
\(\Rightarrow\Delta AME\sim\Delta ACI\left(g-g\right)\Rightarrow\dfrac{AM}{AC}=\dfrac{AE}{AI}\Rightarrow AE.AC=AM.AI\)
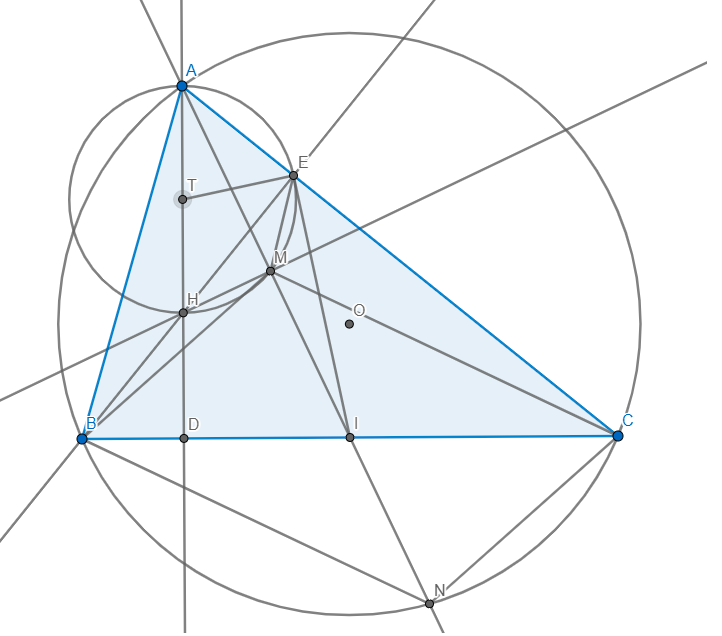
b) Gọi T là trung điểm AH
Dễ dàng chứng minh được T là tâm (AEMH)
\(\Rightarrow\Delta TEH\) cân tại T \(\Rightarrow\angle TEH=\angle THE=\angle ACB\) (HECD nội tiếp)
\(\Delta EBC\) vuông tại E có I là trung điểm BC cân tại I
\(\Rightarrow\Delta EBI\) cân tại I \(\Rightarrow\angle BEI=\angle EBI\)
mà \(\angle EBI+\angle ACB=90\Rightarrow\angle BEI+\angle TEH=90\Rightarrow\angle TEI=90\)
\(\Rightarrow IE\) là tiếp tuyến của (AEMH)
\(\Rightarrow\angle IAE=\angle IEM=\angle ICM\) (EMIC nội tiếp)
mà \(\angle IAE=\angle NBC\) (NBAC nội tiếp) \(\Rightarrow\angle ICM=\angle NBC\)
\(\Rightarrow CM\parallel BN\)
Tương tự \(\Rightarrow BM\parallel CN\) \(\Rightarrow BMCN\) là hình bình hành
mà I là trung điểm BC \(\Rightarrow I\) là trung điểm MN
