Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(1-a+a^2\right)\left(1-b+b^2\right)=1-b+b^2-a+ab-ab^2+a^2-a^2b+a^2b^2.\)
\(=\frac{2-2a-2b+2b^2+2ab+2a^2-2ab\left(a+b\right)+2a^2b^2}{2}\)\(=\frac{\left(a-b\right)^2+1+a^2b^2+\left(1-a\right)^2\left(1-b\right)^2}{2}\ge\frac{1+a^2b^2}{2}\)
Tương Tự : \(\left(1-c+c^2\right)\left(1-d+d^2\right)\ge\frac{1+c^2d^2}{2}\)
(1-a+a2) (1-b+b2) = 1-b+b2-a+ab-ab2+a2-a2b+a2b2.
=2-2a-2b+2b2+2ab+2a2-2ab(a+b)+2a2b2 =(a-b)2+1+a2b2+(1-a)2(1-b)2> 1+a2b2 2 2 Tương Tự:(1-c+c2) (1-d+d2) > 1+c2d2 2

bạn vô đây coi bài nào thích hớp thì xem Cho tam giác ABC. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Gọi H là chân đường vuông góc kể từ B đến AD, K là chân đường vuông góc kẻ từ C đến AE a) Chứng minh rằng HK song song với DE b) Tính HK, biết chu vi tam giác ABC bằng 10 cm Bài 2 Cho tam giác ABC, đường trung tuyến AM. Trên tia đối của tia AM lấy điểm N sao cho AN = AM. Gọi K là giao điểm của CA và NB. Chứng minh NK = 1/2 KB... Xem thêm - Tìm với Google

Theo cách dựng ta có CE vừa là đường cao, vừa là phân giác trong tam giác CDK
\(\Rightarrow\Delta CDK\) cân tại C
\(\Rightarrow DC=CK\)
Tương tự ta có: \(BM=DB\)
Mặt khác theo định lý phân giác: \(\dfrac{AB}{AC}=\dfrac{DB}{DC}\Rightarrow AB.DC=AC.DB\)
\(\Rightarrow AB.DC-AC.DB=0\)
Dễ dàng chứng minh bài toán quen thuộc: \(AD^2=AB.AC-BD.DC\)
\(\Rightarrow AD^2=\left(AM-DB\right)\left(AK+DC\right)-DB.DC\)
\(=AM.AK+AM.DC-DB.AK-DB.DC-DB.DC\)
\(=AM.AK+DC\left(AM-DB\right)-DB\left(AK+DC\right)\)
\(=AM.AK+DC.AB-DB.AC\)
\(=AM.AK\)
\(\Rightarrow AK=\dfrac{AD^2}{AM}=4\)

Cho mình hỏi bài này đã được giải chưa vậy? Mình hiện đang giải bài này nhưng mình vẫn chưa thể giải được.

Câu hỏi của Pham Van Hung - Toán lớp 9 - Học toán với OnlineMath
Bạn tham khảo link này nhé!
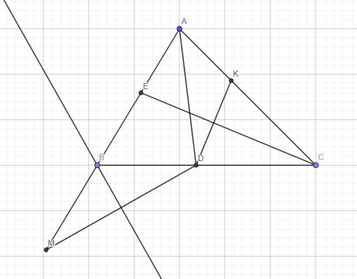
Ta có: \(EF//AM\left(gt\right)\)
\(\Rightarrow\widehat{FEC}=\widehat{AMC}\) (đồng vị)
Xét hai tam giác FEC và AMC có:
\(\widehat{FCE}\) chung
\(\widehat{FEC}=\widehat{AMC}\) (cmt)
\(\Rightarrow\Delta FEC\sim\Delta AMC\) (g.g)
\(\Rightarrow\dfrac{EF}{AM}=\dfrac{CE}{CM}\Rightarrow\dfrac{CM}{AM}=\dfrac{CE}{EF}\) (1)
Chứng minh tương tự ta có: \(\Delta BEG\sim\Delta BMA\left(g.g\right)\)
\(\Rightarrow\dfrac{EG}{AM}=\dfrac{BE}{BM}\Rightarrow\dfrac{CM}{AM}=\dfrac{BE}{EG}\) (vì \(CM=BM\)) (2)
Từ (1) và (2) ta có:
\(\dfrac{CE}{EF}=\dfrac{BE}{EG}\Rightarrow EG\cdot CE=EF\cdot BE\)
\(\Rightarrow EG\cdot\left(BC-BE\right)=EF\cdot BE\)
\(\Rightarrow EG\cdot BC-EG\cdot BE=EF\cdot BE\)
\(\Rightarrow EF\cdot BE+EG\cdot BE=EG\cdot BC\)
\(\Rightarrow EF+EG=\dfrac{EG\cdot BC}{BE}\left(3\right)\)
Từ (2) ta có: \(\dfrac{EG}{AM}=\dfrac{BE}{BM}\)
\(\Rightarrow BM\cdot EG=BE\cdot AM\Rightarrow\dfrac{1}{2}BC\cdot EG=BE\cdot AM\)
\(\Rightarrow EG\cdot BC=2AM\cdot BE\)
\(\Rightarrow2AM=\dfrac{EG\cdot BC}{BE}\left(4\right)\)
Từ (3) và (4) \(\Rightarrow EF+EG=2AM\) (đpcm)