
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ M kẻ ME vuông góc với AB,MF vuông góc với AC.
Ta có ΔEBM vuông cân tại E, ΔFMC vuông cân tại F và AEMF là hình chữ nhật.
Áp dụng định lý Pytago vào các tam giác EBM,FMC,AEF ta có:
BM^2 = EM^2 + BE^2 = 2.ME^2 ; MC^2 = 2.FM^2 ⇒ BM^2 + MC^2 = 2.(ME^2 + MF^2) (1)
Mà AM^2 = EF^2 = ME^2 + MF^2 (2)
Từ (1),(2) ta được 2AM^2 = MB^2 + MC^2

Gọi cạnh của tam giác là a, trung điểm BC là I.
+Ta có: \(BC=a\sqrt{2};\text{ }IB=IC=\frac{IA}{2}=\frac{a}{\sqrt{2}}\)
+Ta có: \(MB^2+MC^2=\left(\frac{a}{\sqrt{2}}-IM\right)^2+\left(\frac{a}{\sqrt{2}}+IM\right)^2=a^2+2IM^2\text{ (1)}\)
+AI vừa là trung tuyến vừa là phân giác góc A nên AI là trung trực tam giác ABC.
=> Tam giác AIM vuông tại I
\(\Rightarrow AM^2=AI^2+IM^2=\left(\frac{a}{\sqrt{2}}\right)^2+IM^2=\frac{a^2}{2}+IM^2\)
\(\Rightarrow2AM^2=a^2+2IM^2\text{ (2)}\)
Từ (1) và (2) suy ra \(MB^2+MC^2=2MA^2\)
Gọi cạnh của tam giác là a, trung điểm BC là I.
+Ta có: BC=a√2; IB=IC=IA2 =a√2
+Ta có: MB2+MC2=(a√2 −IM)2+(a√2 +IM)2=a2+2IM2 (1)
+AI vừa là trung tuyến vừa là phân giác góc A nên AI là trung trực tam giác ABC.
=> Tam giác AIM vuông tại I
⇒AM2=AI2+IM2=(a√2 )2+IM2=a22 +IM2
⇒2AM2=a2+2IM2 (2)
Từ (1) và (2) suy ra MB2+MC2=2MA2

Lấy thêm trung điểm K của BC rồi dùng định lý Pytago tính các cạnh MB, MC, MA theo AB, AC, BC, AK
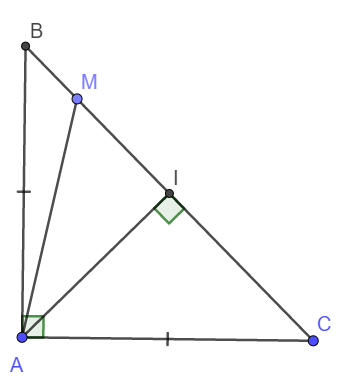
Đặt AB = AC = a \(\Rightarrow BC=\sqrt{AB^2+AC^2}=a\sqrt{2}\)
Gọi I là trung điểm BC, do tam giác ABC cân nên AI cũng là đường cao.
\(AI=BI=IC=\frac{a\sqrt{2}}{2}\)
Đặt MI = x ( 0 < x < \(\frac{a\sqrt{2}}{2}\) )
Ta có \(BM^2=\left(BI-MI\right)^2=\left(\frac{a\sqrt{2}}{2}-x\right)^2\)
\(MC^2=\left(IC+MI\right)^2=\left(\frac{a\sqrt{2}}{2}+x\right)^2\)
\(\Rightarrow MB^2+MC^2=2\left(\frac{a^2}{2}+x^2\right)=2\left(AI^2+MI^2\right)\)
\(=2AM^2\)
Vậy nên ta đã chứng minh được \(\forall M\in BC:BM^2+MC^2=2AM^2\)

tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha

Bài toán phụ: Cho tam giác ABC có \(\widehat{A}=120^o\). Khi đó BC2=AB2+AC2+AB.AC
Chứng minh: Gọi H là hình chiếu của C trên AB
\(AH=\frac{1}{2}AC;CH=\frac{\sqrt{3}}{2}AC\left(1\right)\)
Theo định lý Pytago, ta có: BC2=BH2+CH2 (2)
Từ (1)(2) => BC2=(AB+AH)2+CH2=\(\left(AB+\frac{1}{2}AC\right)^2+\left(\frac{\sqrt{3}}{2}AC\right)^2\)
\(=AB^2+AB\cdot AC+\frac{1}{4}AC^2+\frac{3}{4}AC^2=AB^2+AC^2+AB\cdot AC\)
Không mất tính tổng quát giả sử M thuộc cung \(\widebat{BC}\) (không chứa A) của (O)
Chứng minh được MA=MB+MC
=> MA2=MB2+MC2+2.MB.MC
=> MA2+MB2+MC2=2(MB2+MC2+MB.MC)(3)
Theo BĐ1 ta có: MB2+MC2+MB.MC=BC2
=> MB2+MC2+MB.MC=3R2
Từ (1) (2) => MA2+MB2+MC2=6R2

Cho tam giác ABC vuông tại A, M là trung điểm của AC. Vẽ MD vuông góc với BC ( D thuộc BC ) . Chứng minh : AB2 = BD2 - CD2 .
H là điểm như thế nào vậy bạn?