Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có AB=AM+MB=11+8=19 (cm)
xát tgAMN và tgABC có gA chung
gAMN = gABC (hai góc đồng vị của MN//BC)
=>tgAMN ~ tgABC (g.g)
=>AM/AB=AN/AC=>11/19=AN/38
=>AN=22 (cm)
ta có AC=AN+NC=>NC = 38-22=16(cm)

a: Xét ΔABC có MN//BC
nên AM/MB=AN/NC
=>NC=6(cm)
b: Xét ΔABC có MN//BC
nên ΔAMN∼ΔABC
Suy ra: \(\dfrac{S_{AMN}}{S_{ABC}}=\left(\dfrac{AM}{AB}\right)^2=\left(\dfrac{4}{7}\right)^2=\dfrac{16}{49}\)

Do N nằm giữa A và C nên: NC = AC - AN = 13,5 - 6 = 7,5cm
Ta có:
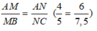
Suy ra: MN // BC ( định lí Ta let đảo)
Theo hệ quả định lí ta let ta có;
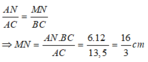
Chọn đáp án B

Xét tam giác ABC và MN//BC
Hai tam giác AMN và ABC, có:
- góc AMN = góc ABC (đồng vị)
- góc ANM = góc ACB (đồng vị)
- BAC là góc chung
Mặt khác, theo hệ quả định lí Ta-lét, hai tam giác AMN và ABC có 3 cặp cạnh tương ứng tỉ lệ:
\(\frac{AM}{AB}=\frac{MN}{BC}=\frac{AN}{AC}\)
Nên tam giác AMN đồng dạng với tam giác ABC
\(\Rightarrow\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{3}\)
\(\Rightarrow\frac{AN}{18}=\frac{1}{3}\)
\(AN=\frac{18.1}{3}=6\)
Do AC = AN + NC
\(\Rightarrow NC=AC-AN=18-6=12\)
Vậy NC có độ dài là 12 cm

a: Xét ΔCAB có CM/CA=CN/CB
nênMN//AB
b: Xét ΔCAB có MN//AB
nên MN/AB=CM/CA
=>MN/6=1/4
=>MN=1,5cm
c: góc CMD=góc CHD=90 độ
=>CMHD nội tiếp
=>góc AMH=góc ADC
Xét ΔAMH và ΔADC có
góc AMH=góc ADC
góc A chung
=>ΔAMH đồng dạng với ΔADC

a: Xét ΔABC có DM//BC
nên \(\dfrac{AD}{AB}=\dfrac{AM}{AC}\)
=>\(\dfrac{AM}{AC}=\dfrac{1}{3}\)
=>\(\dfrac{2}{AC}=\dfrac{1}{3}\)
=>AC=6(cm)
Xét ΔABC có DM//BC
nên \(\dfrac{DM}{BC}=\dfrac{AD}{AB}\)
=>\(\dfrac{4}{BC}=\dfrac{1}{3}\)
=>\(BC=3\cdot4=12\left(cm\right)\)
b: bạn ghi lại đề nha bạn