Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath

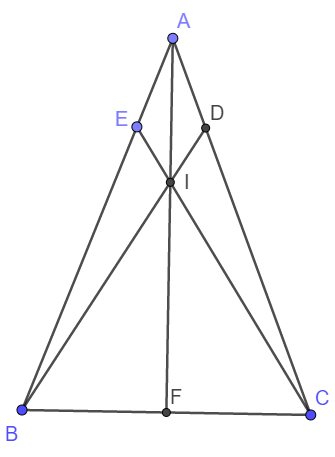
a) Xét tam giác ADB và AEC có:
AD = AE (gt)
AB = AC (gt)
Góc A chung
\(\Rightarrow\Delta ADB=\Delta AEC\left(c-g-c\right)\Rightarrow BD=CE\)
b) Do AB = AC; AD = AE nên BE = DC
Xét tam giác CEB và BDC có:
CE = BD (cma)
Cạnh BC chung
BC = CD (cmt)
\(\Rightarrow\Delta CEB=\Delta BDC\left(c-c-c\right)\)
c) Do \(\Delta ADB=\Delta AEC\Rightarrow\widehat{EBI}=\widehat{DCI}\)
Do \(\Delta CEB=\Delta BDC\Rightarrow\widehat{BEI}=\widehat{CDI}\)
Xét tam giác BIE và tam giác CID có:
\(\widehat{EBI}=\widehat{DCI}\)
\(\widehat{BEI}=\widehat{CDI}\)
BE = CD
\(\Rightarrow\Delta BIE=\Delta CID\left(g-c-g\right)\)
d) Do \(\Delta BIE=\Delta CID\Rightarrow IB=IC\)
Lại có AB = AC nên IA là trung trực của BC
Vậy IA đi qua trung điểm F của BC hay A, I, F thẳng hàng.

Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath

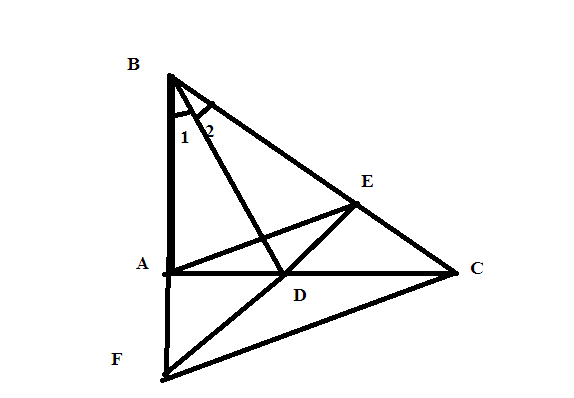
Xét ΔBAD và ΔBDE có:
BD là cạnh chung
B1=B2 (BD là tia phân giác của \(\widehat{B}\))
BA = BE (GT)
Nên ΔBAD= ΔBDE (c.g.c)
=>\(\widehat{ADB}=\widehat{BDE}\)
Ta có:\(\widehat{ADB}+\widehat{ADF}=\widehat{BDF}\)
\(\widehat{BDE}+\widehat{EDC}=\widehat{BDC}\)
Mà :\(\widehat{ADB}=\widehat{BDE}\)(CMT)
\(\widehat{ADF}=\widehat{EDC}\)( 2 góc đối đỉnh)
=>\(\widehat{BDF}=\widehat{BDC}\)
Xét ΔBDF và Δ BDC, có:
\(\widehat{BDF}=\widehat{BDC}\)
BD là cạnh chung
B1=B2
Nên ΔBDF=ΔBDC (g.c.g)
=>DC = DF
b)Ta có:ΔEDC vuông tại E=> DC là cạnh lớn nhất hay DC>DE
MÀ DE=AD (ΔBAD và ΔBDE)
=> AD< DC
c) Ta có BE=BA=>ΔBEA cân tại B
Mà BD là tia phân giác=>BD là đường trung trực
Vì :ΔBDF=ΔBDC=>BF=BC
=>ΔBFC cân tại B=>\(\widehat{C}=\widehat{F}\)
Ta có:\(\widehat{B}+\widehat{C}+\widehat{F}=180^o\)
=>\(\widehat{B}+\widehat{C}.2=180^O\)
=>\(\widehat{C}=\dfrac{180^O-\widehat{B}}{2}\)(1)
vÌ ΔBAE cân tại B
Tương tự ta có:
\(\widehat{E}=\dfrac{180^o-\widehat{B}}{2}\)(2)
Từ (1) và (2)=> \(\widehat{E}=\widehat{C}\)
Mà 2 góc này ở vị trí đồng vị=>AE // FC

