Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC ở D; E là 1 điểm nằm trên cạnh BC sao cho BE = BA. a) CM:...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

vân nguyễn

5 tháng 8 2021

Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC ở D; E là 1 điểm nằm trên cạnh BC sao cho BE = BA.

a) CM: DE vuông góc với BC

b) Gọi F là giao điểm của DE và AB. CMR DE = DF

c) CM: AD<DC

d) CM BD là đường trung trực của AE và AE // FC

#Toán lớp 7

Phạm Vĩnh Linh

5 tháng 8 2021

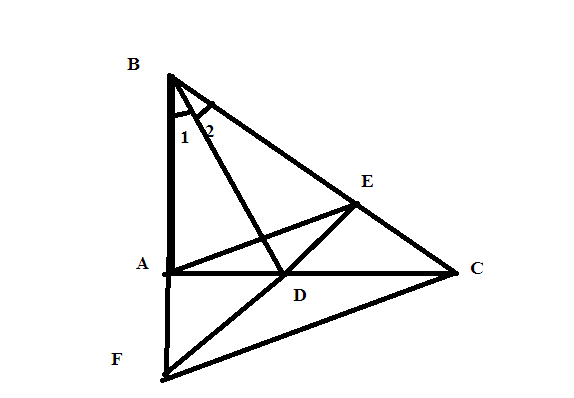
undefined

Đúng(0)

Phạm Vĩnh Linh

5 tháng 8 2021

undefined

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Trần Lạc Băng

3 tháng 8 2021

Cho tam giác ABC vuông tại A . Tia phân giác của góc B cắt AC ở D, E là điểm trên cạnh BC sao cho BE = BA .

a) gọi F là giao điểm của DE và AB . chứng minh rằng DC = DF

b) Chứng minh AD< DC

c) Chứng minh BD là đường trung trực của AE và AE // FC

#Toán lớp 7

Phạm Vĩnh Linh

3 tháng 8 2021

undefined

Xét ΔBAD và ΔBDE có:

BD là cạnh chung

B₁=B₂ (BD là tia phân giác của \(\widehat{B}\))

BA = BE (GT)

Nên ΔBAD= ΔBDE (c.g.c)

=>\(\widehat{ADB}=\widehat{BDE}\)

Ta có:\(\widehat{ADB}+\widehat{ADF}=\widehat{BDF}\)

\(\widehat{BDE}+\widehat{EDC}=\widehat{BDC}\)

Mà :\(\widehat{ADB}=\widehat{BDE}\)(CMT)

\(\widehat{ADF}=\widehat{EDC}\)( 2 góc đối đỉnh)

=>\(\widehat{BDF}=\widehat{BDC}\)

Xét ΔBDF và Δ BDC, có:

\(\widehat{BDF}=\widehat{BDC}\)

BD là cạnh chung

B₁=B₂

Nên ΔBDF=ΔBDC (g.c.g)

=>DC = DF

b)Ta có:ΔEDC vuông tại E=> DC là cạnh lớn nhất hay DC>DE

MÀ DE=AD (ΔBAD và ΔBDE)

=> AD< DC

Đúng(2)

Phạm Vĩnh Linh

3 tháng 8 2021

c) Ta có BE=BA=>ΔBEA cân tại B

Mà BD là tia phân giác=>BD là đường trung trực

Vì :ΔBDF=ΔBDC=>BF=BC

=>ΔBFC cân tại B=>\(\widehat{C}=\widehat{F}\)

Ta có:\(\widehat{B}+\widehat{C}+\widehat{F}=180^o\)

=>\(\widehat{B}+\widehat{C}.2=180^O\)

=>\(\widehat{C}=\dfrac{180^O-\widehat{B}}{2}\)(1)

vÌ ΔBAE cân tại B

Tương tự ta có:

\(\widehat{E}=\dfrac{180^o-\widehat{B}}{2}\)(2)

Từ (1) và (2)=> \(\widehat{E}=\widehat{C}\)

Mà 2 góc này ở vị trí đồng vị=>AE // FC

Đúng(0)

Đặng Công Khánh Toàn

14 tháng 5 2021 - olm

Cho tam giác ABC vuông tại acos phân giác BD ( D thuộc AC) . Trên cạnh BC lấy điểm E sao cho AB= BE .Trên tia đối của tia AB lấy điểm f sao cho Af= EG gọi I là giao điểm của BD với Fc .CM

a, tam giác ABD = tam gác EBD và DE vuông góc BC

B, BD là đường trung trực của đoạn thẳng AE

c, BA điểm D,E,F thẳng hàng

d, Điểm d cách đều ba cạnh của tam giác AEI

#Toán lớp 7

Lê Duy Tâm

7 tháng 2 2019 - olm

Cho tam giác ABC vuông tại A ( AB>AC). Tia phân giác của góc B cắt AC ở E . Trên BC lấy điểm D sao cho BD bằng BA. Đường thẳng DE cắt đương thẳng AB tại F

a) CM ED vuông góc với BC

b)CMR tam giác CF cân tại B

c)Gọi H là giao điểm của BE và FC. Tính BC biết BH= 8cm, FC= 12cm

d)CM AD // FC

#Toán lớp 7

Lê Duy Tâm

9 tháng 2 2019 - olm

Cho tam giác ABC vuông tại A ( AB>AC). Tia phân giác của góc B cắt AC ở E . Trên BC lấy điểm D sao cho BD bằng BA. Đường thẳng DE cắt đương thẳng AB tại F

a) CM ED vuông góc với BC

b)CMR tam giác CF cân tại B

c)Gọi H là giao điểm của BE và FC. Tính BC biết BH= 8cm, FC= 12cm

d)CM AD // FC

#Toán lớp 7

Linh Linh

9 tháng 2 2019

a)Xét ΔABD và ΔEBD có:

AB=BE(gt)

ABDˆ=EBDˆ(gt)ABD^=EBD^(gt)

BD:cạnh chung

=> ΔABD=ΔEBD(c.g.c)

=> BADˆ=BEDˆ=90oBAD^=BED^=90o

=> DE⊥BCDE⊥BC

Vì: ΔABD=ΔEBD(cmt)

=>AD=DE

Vì: AB=BE(gt) ; AD=DE(cmt)

=> B,D thuộc vào đường trung trực của đt AE

=>BD là đường trung trực của đt AE

=>AE⊥BDAE⊥BD

b) Xét ΔDEC vuông tại E(cmt)

=> DE<DCDE<DC

Mà: DE=AD

=> AD<DC

c)Vì: BF=BA+AF ; BC=BE+EC

Mà: BF=BC(gt); BE=BA(gt)

=>AF=EC

Xét ΔADF và ΔEDC có:

AF=EC(cmt)

FADˆ=DECˆ=90o(cmt)FAD^=DEC^=90o(cmt)

AD=DE(cmt)

=>ΔADF=ΔEDC(c.g.c)

Đúng(0)

Lê Duy Tâm

7 tháng 2 2019 - olm

Cho tam giác ABC vuông tại A ( AB>AC). Tia phân giác của góc B cắt AC ở E . Trên BC lấy điểm D sao cho BD bằng BA. Đường thẳng DE cắt đương thẳng AB tại F

a) CM ED vuông góc với BC

b)CMR tam giác CF cân tại B

c)Gọi H là giao điểm của BE và FC. Tính BC biết BH= 8cm, FC= 12cm

d)CM AD // FC

#Toán lớp 7

Nguyễn Tiến Quân

7 tháng 7 2016 - olm

Cho tam giác ABC vuông tại A, đường cao AH, trên BC lấy D sao cho BD = BA. Vẽ đường vuông góc với BC tại D cắt Ac ở E

a) CMR AE = DE

b) CM BE là đường trung trực của AD

c) gọi I là giao điểm của AH và BE. CM DI song song với AC

d) CM : AB + AC < BC + 2AH

#Toán lớp 7

Vu Quang Huy

18 tháng 10 2018 - olm

Cho tam giác ABC vuông tại A, tia phân giác của góc ABC cắt cạnh AC tại D; E là điểm trên cạnh BC sao cho BA = BE

a) Chứng minh tam giác ABD = tam giác EBD

b) Chứng minh rằng DE vuông góc với BC

c) Gọi F là giao điểm của DE với AB. CMR DF=DC

d) Chứng minh BD vuông góc FC

e) Chứng minh AE song song FC

#Toán lớp 7

Vu Quang Huy

18 tháng 10 2018

giúp mình gấp với, còn c, d, e thôiiii

Đúng(0)

Thanh Lương

3 tháng 5 2021

Cho tam giác ABC có AB=3cm, AC=4cm, BC=5cm a) tam giác ABC là tam giác gì? b)Vẽ BD là phân giác góc B. Trên cạnh Bc lấy điểm E sao cho AB=AE. Chứng minh AD=DE c) Cm AE vuông góc BD d) Kéo dài BA cắt ED tại F. Cm AE vuông góc với FC

#Toán lớp 7

Mon an

10 tháng 12 2023

Cho tam giác ABC có góc A =90 độ , BD là tia phân giác của góc B( D thuộc AC ) . Trên cạnh BC lấy điểm E sao cho BA=BE . a) cm : tam giác ABD = tam giác EBD b) trên tia đối của DE lấy F sao cho DC=DF . Cm AF=CE c) Tia BD cắt FC tại H .Cm...

Đọc tiếp

#Toán lớp 7

Nguyễn Lê Phước Thịnh

10 tháng 12 2023

a: Xét ΔABD và ΔEBD có

BA=BE

\(\widehat{ABD}=\widehat{EBD}\)

BD chung

Do đó: ΔABD=ΔEBD

b: ΔABD=ΔEBD

=>\(\widehat{BAD}=\widehat{BED}\)

mà \(\widehat{BAD}=90^0\)

nên \(\widehat{BED}=90^0\)

Xét ΔDAF và ΔDEC có

DA=DE

\(\widehat{ADF}=\widehat{EDC}\)

DF=DC

Do đó: ΔDAF=ΔDEC

=>AF=CE

c: Ta có: ΔDAF=ΔDEC

=>\(\widehat{DAF}=\widehat{DEC}\)

mà \(\widehat{DEC}=90^0\)

nên \(\widehat{DAF}=90^0\)

Ta có: \(\widehat{BAD}+\widehat{DAF}=\widehat{BAF}\)

=>\(\widehat{BAF}=90^0+90^0=180^0\)

=>B,A,F thẳng hàng

Xét ΔBFC có BA/AF=BE/EC

nên AE//FC

Đúng(2)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP