Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2: Xét tứ giác ABDE có
C là trung điểm của BE
C là trung điểm của AD
Do đó: ABDE là hình bình hành
Suy ra: AB//DE

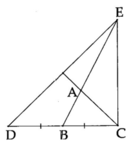
a) Ta có BD = BC, do đó EB là đường trung tuyến của tam giác CDE .
Mặt khác AE = 2AB nên A là trọng tâm của tam giác CDE.
b) Vì A là trọng tâm của tam giác CDE nên CA là đường trung tuyến, suy ra ĐPCM

a: Xét ΔABC và ΔDEC có
CA=CD
\(\widehat{ACB}=\widehat{DCE}\)
CB=CE
Do đó:ΔACB=ΔDCE
b: Xét tứ giác ABDE có
C là trung điểm của AD
C là trung điểm của BE
Do đó: ABDE là hình bình hành
Suy ra: AB//DE
c: Xét ΔAMC và ΔDNC có
AM=DN
\(\widehat{MAC}=\widehat{NDC}\)
AC=DC
Do đó: ΔAMC=ΔDNC
d: Xét tứ giác AMDN có
AM//DN
AM=DN
Do đó: AMDN là hình bình hành
Suy ra: Hai đường chéo AD và MN cắt nhau tại trung điểm của mỗi đường
mà C là trung điểm của AD
nên C là trung điểm của MN
https://hoc24.vn/cau-hoi/1cho-tam-giac-abc-co-2-duong-trung-tuyen-bm-va-cn-cat-nhau-tai-g-chung-minh-bm-cn-dfrac32bc2cho-tam-giac-abc-d-la-trung-diem-ac-tren-bd-lay-e-sao-cho-be2ed-f-thuoc-tia-doi-cua-tia.5863553679489
trl câu này hộ mik với chiều nay cần dùng r![]()

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
DO đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK và AH=AK
Xét ΔADE có
AH/AD=AK/AE
nên HK//DE
hay HK//BC
c: Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{HBD}=\widehat{KCE}\)
Do đó: ΔHBD=ΔKCE
Suy ra: \(\widehat{HBD}=\widehat{KCE}\)
=>\(\widehat{OCB}=\widehat{OBC}\)
=>ΔOBC cân tại O
=>OB=OC
mà HB=CK
nên OB+HB=OC+CK
=>OH=OK
hay ΔOHK cân tại O

a) Tam giác ABC cân tại A (gt) \(\Rightarrow\widehat{ABC}=\widehat{ACB}\) (Tính chất tam giác cân).
Mà \(\left\{{}\begin{matrix}\widehat{ABC}+\widehat{ABD}=180^o.\\\widehat{ACB}+\widehat{ACE}=180^o.\end{matrix}\right.\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}.\)
Xét tam giác ABD và tam giác ACE:
+ AB = AC (Tam giác ABC cân tại A).
+ \(\widehat{ABD}=\widehat{ACE}\left(cmt\right).\)
+ BD = CE (gt).
\(\Rightarrow\) Tam giác ABD = Tam giác ACE (c - g - c).
\(\Rightarrow\) AD = AE (Cặp cạnh tương ứng).
\(\Rightarrow\) Tam giác ADE cân tại A (đpcm).
b) Tam giác ADE cân tại A (cmt). \(\Rightarrow\widehat{ADE}=\widehat{AED}\) (Tính chất tam giác cân).
Xét tam giác DHB và tam giác EKC (\(\widehat{DHB}=\widehat{EKC}=90^o\)) :
+ \(\widehat{HDB}=\widehat{KEC}\) (\(\widehat{ADE}=\widehat{AED}\)).
+ BD = CE (gt).
\(\Rightarrow\) Tam giác DHB = Tam giác EKC (cạnh huyền - góc nhọn).
\(\Rightarrow\) BH = CK (Cặp cạnh tương ứng).
Ta có: \(\left\{{}\begin{matrix}AH+HD=AD.\\AK+KE=AE.\end{matrix}\right.\)
Mà HD = KE (Tam giác DHB = Tam giác EKC); AD = AE (cmt).
\(\Rightarrow\) AH = AK \(\Rightarrow\) Tam giác AHK cân tại A. \(\Rightarrow\) \(\widehat{AHK}=\left(180^o-\widehat{A}\right):2.\)
Mà \(\widehat{ADE}=\left(180^o-\widehat{A}\right):2\) (Tam giác ADE cân tại A).
\(\Rightarrow\) \(\widehat{AHK}=\widehat{ADE}.\)
Mà 2 góc này ở vị trí đồng vị.
\(\Rightarrow\) HK // BC (dhnb).
c) Tam giác DHB = Tam giác EKC (cmt). \(\Rightarrow\) \(\widehat{HBD}=\widehat{KCE}\) (2 góc tương ứng).
Mà \(\widehat{HBD}=\widehat{CBO}\); \(\widehat{KCE}=\widehat{BCO}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{BCO}=\widehat{CBO}\). \(\Rightarrow\) Tam giác OBC là tam giác cân tại O.
d) Xét tam giác ABC cân tại A có: AM là trung tuyến (M là trung điểm BC).
\(\Rightarrow\) AM là đường cao (Tính chất các đường trong tam giác cân).
\(\Rightarrow\) \(AM\perp BC.\) (1)
Xét tam giác OBC cân tại O: OM là trung tuyến (M là trung điểm BC).
\(\Rightarrow\) OM là đường cao (Tính chất các đường trong tam giác cân).
\(\Rightarrow\) \(OM\perp BC.\) (2)
Từ (1) và (2) \(\Rightarrow\) 3 điểm O; A; M thẳng hàng.
\(\Rightarrow\) \(M\in AO.\)
Mà O là giao điểm của BH; CK (gt).
\(\Rightarrow\) O là giao điểm của AM; BH; CK.
\(\Rightarrow\) AM; BH; CK đồng quy (đpcm).

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath
1. a) Vì tam giác ABC cân tại A =>B=ACD Mà ACD=ECN(đối đỉnh) =>B=ECN Vì AB=AC(tam giác ABC cân tại A) Mà AC=IC =>AB=IC Xét tam giác ABD và tam giác ICE có: AB=IC(c/m trên) B=ECN(c/m trên) BD=CE(gt) =>tam giác ABD=tam giác ICE(c.g.c) 2. Xét tam giác BMD và tam giác CEN có: BDM=CNE(=90 độ) BD=CE(gt) B=ECN(c/m trên) =>tam giác BDM=tam giác CEN(g.c.g) =>BM=CN(2 cạnh tương ứng)

a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
b: Xét ΔAHB vuông tại H và ΔACK vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
=>BH=CK và AH=AK
Xét ΔADE co AH/AD=AK/AE
nên HK//DE
=>HK//BC
c: góc HBD+góc D=90 độ
góc KCE+góc E=90 độ
mà góc D=góc E
nên góc HBD=góc KCE
=>góc OBC=góc OCB
=>OB=OC
=>O nằm trên trung trực của BC(1)
ΔBCA cân tại A
mà AM là trung tuyến
nên AM là trung trực của BC(2)
Từ (1), (2) suy ra A,M,O thẳng hàng