Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
HB=15^2/25=9cm
=>HC=16cm
b: Xét ΔCAB vuông tại A và ΔAHB vuông tại H có
góc B chung
=>ΔCAB đồng dạng với ΔAHB
c: Xét ΔABC vuôg tại A co AH là đường cao
nen AH^2=HB*HC
d: góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
=>AH cắt MN tại trung điểm của mỗi đường
=>M,I,N thẳng hàng
e: AM*AB=AH^2
AN*AC=AH^2
=>AM*AB=AN*AC

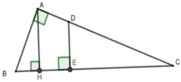
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và A H C ^ = B A C ^ = 90 ∘ nên ΔAHC ~ ΔBAC (g-g)
Ta có S D E C = 1 2 S A B C (1), S A H C : S A B C = H C B C = 9 9 + 3 , 5 = 18 25 2
Từ (1) và (2) suy ra S D E C : S A H C = 1 2 : 18 25 = 25 36 = ( 5 6 ) 2 ( 3 )
Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên
S D E C : S A H C = ( E C H C ) 2 ( 4 )
Từ (3) và (4) suy ra E C H C = 5 6 tức là E C 9 = 5 6 => EC = 7,5cm.
Đáp án: D

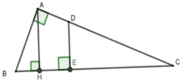
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và A H C ^ = B A C ^ = 90 ∘ nên ΔAHC ~ ΔBAC (g-g)
Ta có S D E C = 1 2 S A B C (1), S A H C : S A B C = 18 25 (2).
Từ (1) và (2) suy ra
S D E C : S A H C = 1 2 : 18 25 = 25 36 = ( 5 6 ) 2 3
Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên
S D E C : S A H C = ( E C H C ) 2 (4)
Từ (3) và (4) suy ra E C H C = 5 6 tức là E C 18 = 5 6 => EC = 15cm.
Đáp án: A

a: Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC
b: \(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
=>AC=20(cm)
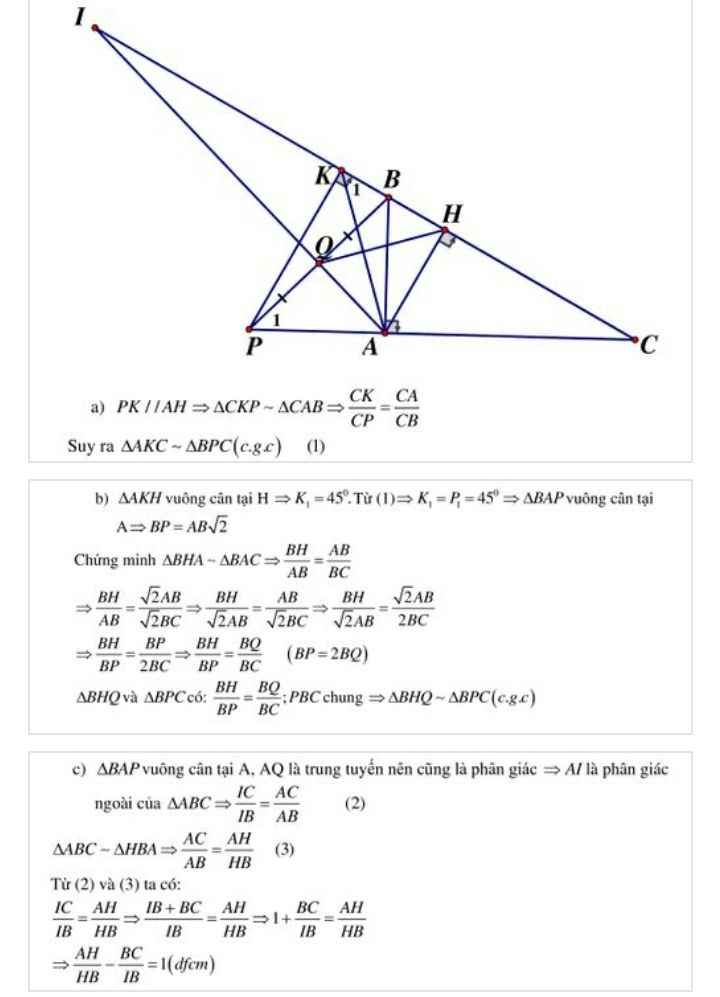


Áp dụng Menelaus:
\(\dfrac{AK}{BK}\cdot\dfrac{BH}{CH}\cdot\dfrac{CI}{AI}=1\Leftrightarrow\dfrac{1}{2}\cdot\dfrac{BH}{HC}\cdot1=1\\ \Leftrightarrow\dfrac{BH}{HC}=2\Leftrightarrow\dfrac{HC}{HB}=\dfrac{1}{2}\)