Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi góc BAC = 60º và BM = CN = BC
Tam giác cân ABC có góc BAC = 60º nên là tam giác đều
⇒ AB = BC và góc B1 = 60º
Ta có: AB = CB, BC = BM (gt) ⇒ AB = BM ⇒ ΔABM cân ở B ⇒ 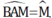
Mà theo tính chất góc ngoài trong ΔBAM thì
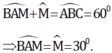
Tương tự ta có
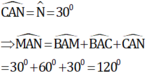
* Ta chứng minh tam giác OBC là tam giác đều.
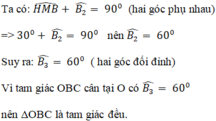

Xét tam gia ABM va ANC co:
AB = AC(gt)
\(\widehat{B}\) =\(\widehat{C}\) (gt)
BM =NC (gt)
=> \(\Delta\) ABM =\(\Delta\) ANC (C.G.C)

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath

a: Xét ΔMHB vuông tại H và ΔNKC vuông tại K có
BM=CN
\(\widehat{B}=\widehat{C}\)
Do đó: ΔMHB=ΔNKC
b: Ta có: ΔMHB=ΔNKC
nên HB=KC
Ta có: AH+HB=AB
AK+KC=AC
mà BA=AC
và HB=KC
nên AH=AK
c: Xét ΔAHM vuông tại H và ΔAKN vuông tại K có
AH=AK
HM=KN
Do đó: ΔAHM=ΔAKN
Suy ra: AM=AN

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath

Ta có: BM = AB (gt) => tam giác ABM cân tại B => \(\widehat{BMA}=\widehat{BAM}=\frac{180^0-\widehat{B}}{2}=\frac{180^0-60^0}{2}=60^0\)
Xét tam giác ABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) => \(\widehat{C}=180^0- \left(\widehat{A}+\widehat{B}\right)=180^0-80^0-60^0=40^0\)
Lại có: AC = AC (gt) => tam giác ANC cân tại C => \(\widehat{ANC}=\widehat{NAC}=\frac{180^0-40^0}{2}=70^0\)
Xét tam giác AMN có: \(\widehat{MAN}+\widehat{AMN}+\widehat{ANM}=180^0\) => \(\widehat{MAN}=180^0-60^0-70^0=50^0\)
Vậy ...