Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

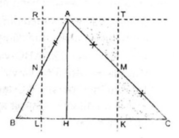
Xét △ ABC. Kẻ đường cao AH. Gọi M là trung điểm của AC, N là trung điểm của AB.
Từ M kẻ đường thẳng song song AH cắt BC tại K
Từ N kẻ đường thẳng song song AH cắt BC tại L
Từ A kẻ đường thẳng song song BC cắt hai đường thẳng MK và NL tại T và R
Ta có: △ MKC = △ MTA
△ NLB = △ NAR
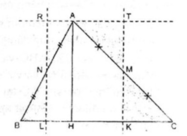
Cắt △ ABC theo đường MK và NL ta ghép lại được một hình chữ nhật KTRL có diện tích bằng diện tích tam giác ABC

a. Xét tam giác ABC vuông tại A có:
AB2+AC2=BC2 (định lý Py-ta-go)
=>62+AC2=BC2
=>AC=8 cm.
=> SABC=AB.AC=6.8=48 (cm)
b. Ta có: SABC=AB.AC=BC.AH
=>6.8=10.AH
=>AH=4,8 cm.
a/
diện tích tam giác ABC là:
\(\dfrac{6.10}{2}\)=30 (cm2)
đường cao AH là
30:10=3 cm

Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~

a: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc HBA chung
Do đó: ΔABD\(\sim\)ΔHBA
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
\(HB=\dfrac{AB^2}{BD}=6.4\left(cm\right)\)

a: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc HBA chung
Do đó: ΔABD\(\sim\)ΔHBA
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
\(HB=\dfrac{AB^2}{BD}=6.4\left(cm\right)\)

a. Có: tam giác ABC vuông tại A (gt)
=> góc BAC = 90o
Có: AH là đường cao của tam giác ABC (gt)
=> góc AHB = góc AHC = 90o
Xet tam giác HBA và tam giác ABC, có:
góc AHB = góc BAC (=90o)
góc B chung
=> tam giác HBA ~ tam giác ABC (g.g)
b. Xét tam giác ABC vuông tại A, có:
AB2 + AC2 = BC2 (định lý Py-ta-go)
32 + 42 = BC2 (thay số)
BC2 = 25
=> BC = 5
Vậy...



a/
\(S_{\Delta ABC}=\frac{1}{2}.BC.AH=\frac{1}{2}.6.4=12cm^2\)
b/
Gọi D và E lần lượt là trung điểm của AB và AC
Từ B dựng đường thẳng vuông góc BC cắt DE tại M
Từ C dựng đường thẳng vuông góc BC cắt DE tại N
Ta có
DA=DB; EA=EC => DE là đường trung bình của tg ABC => DE//BC => MN//BC
Ta có
\(BM\perp BC;CN\perp BC\)=> BM//CN (cùng vuông góc với BC)
=> BCNM là hình bình hành (tứ giác có các cặp cạnh đối // với nhau là hbh)
Mà \(\widehat{DBC}=90^o\)
=> BCNM là HCN (Hình bình hành có 1 góc vuông là HCN)
Ta có
Gọi I là giao của DE với AH ta có
DE//BC (cmt); \(AH\perp BC\Rightarrow AH\perp DE\)
DE//BC (cmt) \(\Rightarrow\frac{AD}{BD}=\frac{AE}{CE}=\frac{AI}{HI}=1\) => I là trung điểm của AH => IA=IH
Ta có
\(S_{\Delta ABC}=S_{BCED}+S_{\Delta ADI}+S_{AEI}\) (1)
\(S_{BCNM}=S_{BCED}+S_{\Delta BDM}+S_{\Delta CEN}\) (2)
Xét tg vuông ADI và tg vuông BDM có
DA=DB; \(\widehat{ADI}=\widehat{BDM}\) (góc đối đỉnh) => tg ADI = tg BDM (hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau) (3)
C/m tương tự ta cũng có tg AEI = tg CEN (4)
Từ (1) (2) (3) (4) \(\Rightarrow S_{\Delta ABC}=S_{BCNM}\)
=> 3 mảnh cắt từ tg ABC là hình thang BCED; tg ADI và tg AEI
Ta có DE là đường trung bình của tg ABC => \(DE=\frac{BC}{2}=\frac{6}{2}=3cm\)
IA=IH (cmt) => IA=IH=4:2=2 cm
\(S_{BCED}=\frac{\left(BC+DE\right).IH}{2}=\frac{\left(6+3\right).2}{2}=9cm^2\)
\(S_{\Delta ADI}+S_{\Delta AEI}=S_{\Delta ADE}=\frac{1}{2}.DE.IA=\frac{1}{2}.3.2=3cm^2\)
Do tg ABC không có thêm điều kiện nào nên không thể tính riêng rẽ diện tích của hai tg ADI và AEI