Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B D E K O C d1 d2 H I G
a/
\(d_1;d_2\) là tiếp tuyến với đường tròn tại A và B \(\Rightarrow d_1\perp AB;d_2\perp AB\) => \(d_1\)//\(d_2\)
Xét tg vuông ABK có
\(\widehat{ACB}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AK^2=KC.KB\) (Trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu của cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
b/
Ta có
DA=DC (2 tiếp tuyến của 1 đường tròn cùng xuất phát từ 1 điểm thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau) (1)
EC=EB (lý do như trên) => tg EBC cân tại E\(\Rightarrow\widehat{ECB}=\widehat{KBE}\) (2 góc ở đáy của tg cân) (*)
\(\widehat{KBE}=\widehat{AKB}\) (góc so le trong) (**)
\(\widehat{KCD}=\widehat{ECB}\) (Góc đối đỉnh) (***)
Từ (*) (**) và (***) \(\Rightarrow\widehat{AKB}=\widehat{KCD}\) => tg DCK cân tại D => DC=DK (2)
Từ (1) và (2) => DA=DK nên K là trung điểm của AK
c/ Gọi I là giao của CH với BD
Ta có
\(CH\perp AB;d_1\perp AB\) => CH//\(d_1\)
\(\Rightarrow\frac{IC}{DK}=\frac{BC}{BK}=\frac{BH}{BA}=\frac{IH}{DA}\) (Talet trong tam giác)
Mà DK=DA => IC=IH => BD đi qua trung điểm I của CH
d/
câu a ý số 2 bạn còn cách nào khác ko? Tại mk chx hc góc nội tiếp chắn nửa đường tròn

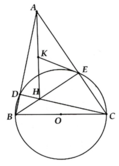
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm