Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét tứ giác BHEK có \(\widehat{BHE}+\widehat{BKE}=180^0\)
nên BHEK là tứ giác nội tiếp
2: Xét ΔBEA vuông tại E có EH là đường cao
nên \(BH\cdot BA=BE^2\left(1\right)\)
Xét ΔBEC vuông tại E có EK là đường cao
nên \(BK\cdot BC=BE^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BA=BK\cdot BC\)

cho tam giác ABC vuông cân tại B.Trên cạnh BA và BC lấy hai điểm E và F sao cho BE = BF.Qua B và E kẻ đường vuông góc với AF,chúng cắt AC lần lượt ở I và K. EK cắt BC tại H
a)Chứng minh tam giác AHC cân
b)chứng minh I là trung điểm KC
c)Gọi M,N,P lần lượt là trung điểm EC,AF,EF

a, HS tự chứng minh
b, HS tự chứng minh
c, HS tự chứng minh
d, ∆MIH:∆MAB
=> M H M B = I H A B = 2 E H 2 F B = E H F B
=> ∆MHE:∆MBF
=> M F A ^ = M E K ^ (cùng bù với hai góc bằng nhau)
=> KMEF nội tiếp => M E F ^ = 90 0


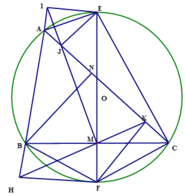
a) Ta có: A I E ^ = A J E ^ = 90 0 nên tứ giác AIEJ nội tiếp.
E M C ^ = E J C ^ = 90 0 nên tứ giác CMJE nội tiếp.
Xét tam giác Δ A E C v à Δ I E M , có
A C E ⏜ = E M I ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác CMJE).
E A C ⏜ = E I M ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác AIEJ).
Do đó hai tam giác Δ A E C ~ Δ I E M đồng dạng
⇒ A E E I = E C E M ⇒ E A . E M = E C . E I (đpcm)




a/ H và K cùng nhìn BE dưới 1 góc vuông nên H và K cùng nằm trên đường tròn đường kính BE
=> BHEK là tứ giác nội tiếp
b/
Xét tg vuông ABE có
\(BE^2=BH.BA\) (Trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu của cạnh góc vuông trên cạnh huyền với cạnh huyền)
Xét tg vuông CBE có
\(BE^2=BK.BC\) (Lý do như trên)
\(\Rightarrow BH.BA=BK.BC\) (đpcm)
c/
Gọi M là giao của BE và CF
Nối H với K cắt EF tại I' và cắt CF tại N
Ta có E và F cùng nhìn BC dưới 1 góc vuông nên E và F cùng nằm trên đường tròn đường kính BC
=> BCEF là tứ giác nội tiếp
\(\Rightarrow\widehat{EBC}=\widehat{EFC}\) (góc nội tiếp cùng chắn cung EC)
Ta có
\(EH\perp AB;CF\perp AB\) => EH//CF \(\Rightarrow\widehat{EFC}=\widehat{HEF}\) (góc so le trong)
\(\Rightarrow\widehat{EBC}=\widehat{HEF}\)
Xét tg vuông HEF và tg vuông EBC có
\(\widehat{EBC}=\widehat{HEF}\) (cmt) \(\Rightarrow\widehat{ECB}=\widehat{HFE}\)
Xét tg vuông MEC có
\(\widehat{ECF}=\widehat{MEN}\) (cùng phụ với \(\widehat{EMC}\) )
Ta có \(\widehat{FEB}=\widehat{FCB}\) (góc nội tiếp cùng chắn cung FB)
\(\Rightarrow\widehat{FEB}+\widehat{MEN}=\widehat{FCB}+\widehat{ECF}\Rightarrow\widehat{FEN}=\widehat{ECB}\)
Mà \(\widehat{ECB}=\widehat{HFE}\) (cmt)
\(\Rightarrow\widehat{FEN}=\widehat{HFE}\) => HF//EN (hai đường thẳng bị cắt bởi 1 đường thẳng tạo thành hai góc so le trong bằng nhau thì chúng // với nhau)
Mà HE//CF (cmt)
=> HENF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau từng đôi 1 là hbh)
=> I'E = I'F (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)
=> I' là trung điểm của EF mà I cũng là trung điểm của EF => I trùng I'
=> H; I; K thẳng hàng
1) \(\widehat{BHE}=\widehat{BKE}=90^o\) nên \(H,K\) cùng nhìn \(BE\) dưới một góc vuông suy ra \(BHEK\) nội tiếp.
2) Xét tam giác \(BEA\) vuông tại \(E\) đường cao \(EH\):
\(BH.BA=BE^2\) (hệ thức trong tam giác vuông)
Tương tự khi xét tam giác \(BEC\) vuông tại \(E\) đường cao \(EK\) cũng có \(BK.BC=BE^2\) suy ra \(BH.BA=BK.BC\).
3) Gọi \(I'\) là giao điểm của \(HK\) và \(EF\). Ta sẽ chứng minh \(I'\) là trung điểm của \(EF\).
\(BFEC\) nội tiếp nên \(\widehat{EFC}=\widehat{EBC}\)
\(BHEK\) nội tiếp nên \(\widehat{EBK}=\widehat{EHK}\)
\(EH//CF\) nên \(\widehat{HEF}=\widehat{EFC}\)
suy ra \(\widehat{EHK}=\widehat{HEF}\) suy ra tam giác \(I'HE\) cân tại \(I'\) suy ra \(I'H=I'E\).
Từ \(\widehat{EHK}=\widehat{HEF}\) ta cũng suy ra \(\widehat{I'HF}=\widehat{I'FH}\) suy ra tam giác \(I'FH\) cân tại \(I'\) nên \(I'H=I'F\) suy ra \(I'F=I'E\) nên \(I'\) là trung điểm của \(EF\).
Suy ra \(I\) và \(I'\) trùng nhau.
Suy ra đpcm.