Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn tự vẽ hinh nha
1)
Xét tam giác ABC có
hai đường cao BE và CD cắt nhau tại H nên H là trực tâm
do đó \(AH\perp BC\)
mà \(HM\perp BC\)
suy ra AH trùng với HM
vậy A; H; M thẳng hàng
b)
dễ chứng minh tam giác BHM đồng dạng với tam giác BCE \(\Rightarrow\frac{BH}{BC}=\frac{BM}{BE}\Rightarrow BH\cdot BE=BC\cdot BM\left(1\right)\)
dễ chứng minh tam giác CHM đồng dạng với tam giác CBD \(\Rightarrow\frac{CH}{BC}=\frac{CM}{CD}\Rightarrow CH\cdot CD=CM\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE+CH\cdot CD=BM\cdot BC+CM\cdot BC=\left(BM+CM\right)\cdot BC=BC\cdot BC=BC^2\)
2)
a)
Xét tam giác ABC và tam giác DEC
có \(\widehat{BAC}=\widehat{CDE}\)
\(\widehat{ACB}\)chung
nên tam giác ABC đồng dạng với tam giác DEC
\(\Rightarrow\frac{AB}{DE}=\frac{AC}{CD}\left(1\right)\)
b)
Xét tam giác ABC
có AD là đường phân giác
\(\Rightarrow\frac{BD}{CD}=\frac{AB}{AC}\Rightarrow\frac{AB}{BD}=\frac{AC}{CD}\left(2\right)\)
Từ (1) và (2) suy ra
\(\frac{AB}{DE}=\frac{AB}{BD}\Rightarrow DE=BD\)

A B C H
a) Xét tam giác HBA và tam giác ABC :
\(\widehat{AHB}=\widehat{BAC}\left(=90^0\right)\)
\(\widehat{ABC}\)chung
=> tam giác HBA \(~\)tam giác ABC ( đpcm )
b) Chứng minh tương tự câu a) ta có tam giác ABC \(~\)tam giác HAC
\(\Rightarrow\frac{AC}{HC}=\frac{BC}{AC}\)
\(\Rightarrow AC^2=HC\cdot BC\)( đpcm )
c) Áp dụng đính lý Pytago vào tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25\)( cm )
Từ câu b) ta có : \(HC=\frac{AC^2}{BC}=\frac{20^2}{25}=16\)
Vậy....

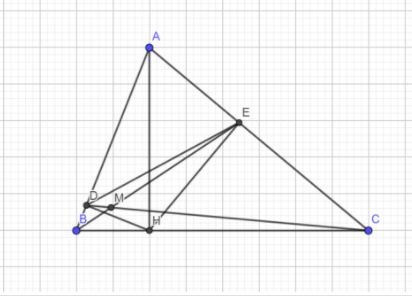
Đoạn thẳng f: Đoạn thẳng [A, C] Đoạn thẳng h: Đoạn thẳng [B, C] Đoạn thẳng i: Đoạn thẳng [B, A] Đoạn thẳng l: Đoạn thẳng [A, M] Đoạn thẳng n: Đoạn thẳng [B, D] Đoạn thẳng p: Đoạn thẳng [C, E] Đoạn thẳng q: Đoạn thẳng [D, E] Đoạn thẳng r: Đoạn thẳng [D, M] Đoạn thẳng s: Đoạn thẳng [M, E] Đoạn thẳng a: Đoạn thẳng [A, H] A = (-0.88, 1.82) A = (-0.88, 1.82) A = (-0.88, 1.82) C = (8.6, 1.86) C = (8.6, 1.86) C = (8.6, 1.86) Điểm B: Điểm trên g Điểm B: Điểm trên g Điểm B: Điểm trên g Điểm M: Điểm trên h Điểm M: Điểm trên h Điểm M: Điểm trên h Điểm D: Giao điểm của j, m Điểm D: Giao điểm của j, m Điểm D: Giao điểm của j, m Điểm E: Giao điểm của k, m Điểm E: Giao điểm của k, m Điểm E: Giao điểm của k, m Điểm H: Giao điểm của t, h Điểm H: Giao điểm của t, h Điểm H: Giao điểm của t, h
a. Ta thấy \(\widehat{DAB}=\widehat{MAC}\) (Cùng phụ với góc \(\widehat{BAM}\)); \(\widehat{DBA}=\widehat{MCA}\)(Cùng phụ với góc \(\widehat{ABM}\))
Vậy nên \(\Delta CAM\sim\Delta BAD\left(g-g\right)\)
b. Do \(\Delta CAM\sim\Delta BAD\left(cma\right)\Rightarrow\frac{AM}{AD}=\frac{AC}{AB}\Rightarrow\frac{AM}{AC}=\frac{AD}{AB}\)
Mà \(\widehat{DAM}=\widehat{BAC}=90^o\Rightarrow\Delta ADM\sim\Delta ABC\left(c-g-c\right)\)
c. Ta thấy \(\widehat{ABM}=\widehat{ACE}\) (Cùng phụ với góc \(\widehat{ACM}\)); \(\widehat{BAM}=\widehat{CAE}\)(Cùng phụ với góc \(\widehat{MAC}\))
Vậy nên \(\Delta BAM\sim\Delta CAE\left(g-g\right)\Rightarrow\frac{AE}{AM}=\frac{AC}{AB}\Rightarrow\frac{AE}{AC}=\frac{AM}{AB}\)
Từ câu b: \(\frac{AD}{AB}=\frac{AM}{AC}\)và ta vừa cm \(\frac{AE}{AC}=\frac{AM}{AB}\Rightarrow\frac{AD.AE}{AB.AC}=\frac{AM^2}{AC.AB}\Rightarrow AD.AE=AM^2\)
d. Do \(AD.AE=AM^2;\widehat{DAM}=\widehat{MAE}=90^o\Rightarrow\Delta DAM\sim\Delta MAE\left(c-g-c\right)\)
\(\Rightarrow\widehat{DMA}=\widehat{MEA}\Rightarrow\widehat{DME}=90^o\). Lại có \(\widehat{EDM}=\widehat{ABC}\Rightarrow\Delta ABC\sim\Delta MDE\left(g-g\right)\)
Để \(\frac{S_{ABC}}{S_{MDE}}=\frac{1}{4}\Rightarrow\) tỉ số đồng dạng \(k=\frac{1}{2}.\)
Gọi AH là đường cao của tam giác ABC, khi đó AM = 2AH \(\Rightarrow\widehat{AMB}=30^o.\)
Vậy M là một điểm thuộc AB sao cho \(\widehat{AMB}=30^o.\)