Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A. \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\) (Loại)
Vì: Theo định lí cos ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
Không đủ dữ kiện để suy ra \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)
B. \(\frac{b}{{\sin A}} = \frac{a}{{\sin B}}\) (Loại)
Theo định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \nRightarrow \frac{b}{{\sin A}} = \frac{a}{{\sin B}}\)
C. \(\sin B = \frac{{ - \sqrt 2 }}{2}\)(sai vì theo câu a, \(\sin B = \frac{{\sqrt 2 }}{2}\))
D. \({b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)
Theo định lý cos ta có:
\({b^2} = {c^2} + {a^2} - 2ca.\cos B\) (*)
Mà \(\widehat B = {135^o} \Rightarrow \cos B = \cos {135^o}\).
Thay vào (*) ta được: \({b^2} = {c^2} + {a^2} - 2ca\;\cos {135^o}\)
=> D đúng.
Chọn D

A. \(\sin A = \sin \,(B + C)\)
Ta có: \((\widehat A + \widehat C) + \widehat B= {180^o}\)
\(\Rightarrow \sin \,(B + C) = \sin A\)
=> A đúng.
B. \(\cos A = \cos \,(B + C)\)
Sai vì \(\cos \,(B + C) = - \cos A\)
C. \(\;\cos A > 0\) Không đủ dữ kiện để kết luận.
Nếu \({0^o} < \widehat A < {90^o}\) thì \(\cos A > 0\)
Nếu \({90^o} < \widehat A < {180^o}\) thì \(\cos A < 0\)
D. \(\sin A\,\, \le 0\)
Ta có \(S = \frac{1}{2}bc.\sin A > 0\). Mà \(b,c > 0\)
\( \Rightarrow \sin A > 0\)
=> D sai.
Chọn A

Theo đl sin có:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}\Rightarrow b=a\dfrac{sinB}{sinA};c=\dfrac{sinC}{sinA}.a\)
Mà `b+c=2a`
\(\Rightarrow a\dfrac{sinB}{sinA}+a\dfrac{sinC}{sinA}=2a\\ \Rightarrow\dfrac{sinB}{sinA}+\dfrac{sinC}{sinA}=2\\ \Leftrightarrow sinB+sinC=2sinA\)
Chọn B

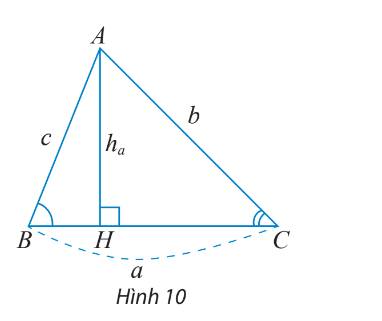
a) Diện tích S của tam giác ABC là: \(S = \frac{1}{2}a.{h_a}\)
b) Xét tam giác vuông AHC ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b}\)
\( \Rightarrow {h_a} = b.\sin C\)
c) Thay \({h_a} = b.\sin C\) vào công thức diện tích, ta được: \(S = \frac{1}{2}ab\sin C\)
d) Theo định lí sin ta có: \(\frac{c}{{\sin C}} = 2R \Rightarrow \sin C = \frac{c}{{2R}}\)
Thay vào công thức ở c) ta được: \(S = \frac{1}{2}ab\frac{c}{{2R}} = \frac{{abc}}{{4R}}.\)

Theo định lí sin trong tam giác ta có:
a sin A = 2 R ⇒ a = 2 R . sin A
Tương tự, b = 2 R . sin B ; c = 2 R . sin C
Ta có: a b = c 2 n ê n 2 R . sin A . 2 R . sin B = ( 2 R sin C ) 2
Hay sin A . sin B = ( sin C ) 2
ĐÁP ÁN A