Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án:
Giải thích các bước giải:
1. Xét tứ giác CEHD có :
CEH = 90 ( BE là đường cao )
CDH = 90 ( AD là đường cao )
⇒ CEH + CDH = 90 + 90 = 180
Mà CEH và CDH là hai góc đối của tứ giác CEHD
⇒ CEHD là tứ giác nội tiếp (đpcm)
2. BE là đường cao ( gt )
⇒ BE ⊥ AB ⇒ BFC = 90
Như vậy E và F cùng nhìn BC dưới một góc 90 ⇒ E và F cùng nằm trên (O) đường kính AB
⇒ 4 điểm B, C, E, F cùng nằm trên một đường tròn (đpcm)
3. Xét ΔAEH và ΔADC có :
AEH = ADC (=90)
A chung
⇒ ΔAEH ~ ΔADC
⇒ AE/AD = AH/AC
⇒ AE.AC = AH.AD
Xét ΔBEC và ΔADC có :
BEC = ADC (=90)
C chung
⇒ ΔBEC ~ ΔADC
⇒ AE/AD = BC/AC
⇒ AD.BC = BE.AC (đpcm)
4. Có : C1 = A1 (cùng phụ góc ABC)
C2 = A1 ( hai góc nối tiếp chắn cung BM )
⇒ C1 = C2 ⇒ CB là tia phân giác HCM
Lại có : CB ⊥ HM
⇒ Δ CHM cân tại C
⇒ CB là đường trung trực của HM
⇒ H và M đối xứng nhau qua BC (đpcm)
5. Có : Bốn điểm B,C,E,F cùng nằm trên một đường tròn ( câu 2 )
⇒ C1 = E1 (hai góc nội tiếp cùng chắn BF) (*)
Có : Tứ giác CEHD nội tiếp (câu 1)
⇒ C1 = E2 (hai góc nội tiếp cùng chắn cung HD ) (**)
Từ (*) và (**) ta suy ra :
E1 = E2
⇒ EB là tia phân giác DEF
Cm tương tự ta được : FC là tia phân giác của DFE
Mà BE và CF cắt nhau tại H
⇒ H là tâm của đường tròn nội tiếp ΔDEF

a, Xét tứ giác BCEF có
^CEB = ^CFB = 900
mà 2 góc này kề, cùng nhìn cạnh BC
Vậy tứ giác BCEF là tứ giác nt 1 đường tròn
b, Xét tứ giác AEHF có
^HEA = ^HFA = 900
Vậy tứ giác AEHF là tứ giác nt 1 đường tròn
c, Ta có ^AMN = ^ACN ( góc nt chắn cung AN )
^ANM = ^MBA ( góc nt chắn cung MA )
mà ^ACN = ^MBA ( tứ giác BCEF nt và 2 góc cùng nhìn cung CF )
=> ^AMN = ^ANM Vậy tam giác AMN cân tại A
=> AN = AM
d, Ta có : ^CBM = ^CFE ( góc nt chắn cung CE của tứ giác BCEF )
mặt khác : ^CNM = ^CBM ( góc nt chắn cung CM )
=> ^CFE = ^CNM, mà 2 góc này ở vị trí đồng vị )
=> MN // EF
e, Ta có AO là đường cao tam giác MAN
mà MN // EF ; AO vuông MN => AO vuông EF

Câu hỏi của hungbck5 - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

a)HEC+HDC=180 => .......
b)BFC=BEC=90 =>tứ giác FEAC noi tiep => .....
c)
- AE*AC=AH*AD thì cm tam giác AEB dong dang tam giác AFC
- 2*S abc = AD*BC=BE*AC

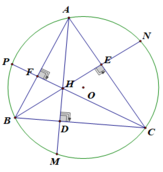
b) Xét tứ giác BFEC có:
∠(BFC) = 90 0 (Do CF là đường cao)
∠(BEC ) = 90 0 (Do BE là đường cao)
⇒ E và F cùng nhìn BC dưới một góc bằng nhau
⇒ Tứ giác BFEC nội tiếp được đường tròn
⇒ Bốn điểm B, E, F, C cùng nằm trên đường tròn