Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta chỉ cần chứng minh \(BD=CE.\) (Thực vậy, khi đó nếu I là trung điểm BC thì BI=EI).
Để cho tiện ta kí hiệu \(a=BC,b=CA,c=AB.\)
Gọi \(D,P,Q\) là tiếp điểm của đường tròn nội tiếp với ba cạnh \(BC,CA,AB.\)
Gọi \(E,R,S\) là tiếp điểm của đường tròn bàng tiếp góc A với ba cạnh \(BC,CA,AB.\)
Ta có \(BD=BQ,CR=CD,AQ=AR\Rightarrow BD+CR+AQ=\frac{a+b+c}{2}\)
Mặt khác \(AR+CR=b\Rightarrow BD=\frac{a+c-b}{2}\). (1)
Theo tính chất tiếp tuyến
\(2AR=AR+AS=AB+AC+BS+CR=AB+AC+BC\Rightarrow AR=\frac{a+b+c}{2}.\)
Do đó \(CE=CR=AR-AC=\frac{a+b+c}{2}-b=\frac{a+c-b}{2}.\) (2)
Từ (1),(2) suy ra \(BD=CE\).

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

Do K đối xứng với D qua trung điểm của BC nên ta có
\(BD=CK,BK=CD\)
Dựng đường kính DF của (I). Theo hình , thì ta được ba điểm A, F , K thẳng hàng
ta có\(\widehat{KDL}=\widehat{DIC}\left(=90^0-\widehat{CID}\right)=>\)tam giác IDC = tam giác DKL (g.g), từ đó suy ra
\(\frac{DF}{DK}=\frac{2ID}{DK}=\frac{2DC}{KL}=\frac{KB}{KN}\)
=> tam giác DFK = tam giác KBN (c.g.c)
zì zậy nên : \(\widehat{KNB}=\widehat{DKF}=90^0-\widehat{NKF}\)
=>\(\widehat{KNB}+\widehat{NKF}=90^0,\)do đó \(AK\perp BN\)

Chú ý góc APC = góc AMC ( t/c đối xứng)
Mà góc AMC = Góc ABC
Chú ý : CH vuông góc AB
Từ đây có ngay kết quả nhe

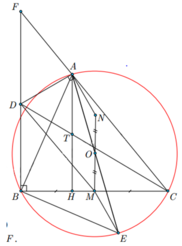
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .

a, xét tứ giác BCDE có:
góc BEC = 90 độ
góc BDC = 90 độ
=>góc BEC=BDC
=>tứ giác BCDE nt
xét tứ giác ADHE có:
góc AEH = 90 độ
góc ADH=90 độ
=>AEH+ADH=180
=>tứ giác ADHE nt
b, vì tứ giác EDCB nt(cmt)
=>góc AED=ACB
xet tam giác AED và ACB có:
góc EAD chung
góc AED=ACB
=>2 tam giác này đồng dạng vs nhau
=>AE/AC=AD/AB
=>AD.AC=AE.AB
C, ta có :góc xAB=ACB
mak góc góc ACB=AED(cmt)
=>góc xAB=AED
=>Ax//ED