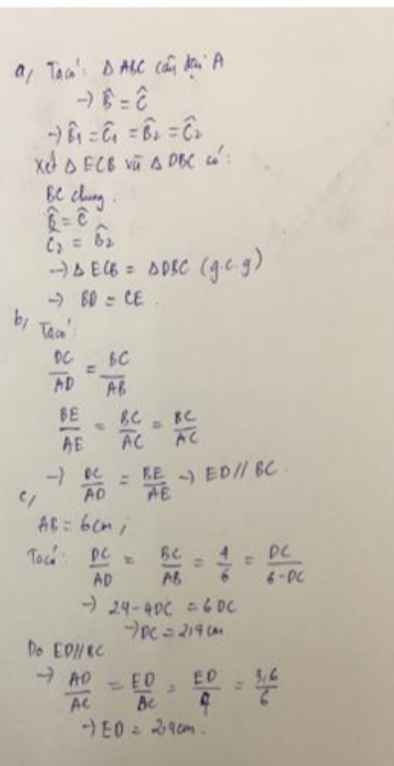Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Xét tam giác $ABD$ và $ACE$ có:
$\widehat{A}$ chung
$AB=AC$ (do tam giác $ABC$ cân tại $A$)
$\widehat{ABD}=\frac{1}{2}\widehat{B}=\frac{1}{2}\widehat{C}=\widehat{ACE}$ (do tam giác $ABC$ cân tại $A$)
$\Rightarrow \triangle ABD=\triangle ACE$ (g.c.g)
$\Rightarrow AD=AE$
Mà $AB=AC$ nên $\frac{AE}{AB}=\frac{AD}{AC}$
$\Rightarrow DE\parallel BC$ (Talet đảo)
Áp dụng định lý Talet:
$\frac{DE}{BC}=\frac{AD}{AC}$
Theo tính chất tia phân giác thì:
$\frac{AD}{DC}=\frac{AB}{BC}=\frac{b}{a}$
$\Rightarrow \frac{AD}{AC}=\frac{b}{a+b}$
Do đó: $\frac{DE}{BC}=\frac{b}{a+b}$
$\Rightarrow DE=BC.\frac{b}{a+b}=\frac{ab}{a+b}$

Bài 1 : Bài giải
a, Trong \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\text{ }\Rightarrow\text{ }9^2+12^2=81+144=225=BC^2\text{ }\Rightarrow\text{ }BC=5\text{ }cm\)
b, Vì BD là đường phân giác \(\widehat{ABC}\) nên : \(\widehat{B_1}=\widehat{B_2}\)
Xét 2 tam giác \(\Delta ABD\) vuông tại A và \(\Delta AED\) vuông tại E có :
\(BD\) : cạnh huyền - cạnh chung
\(\widehat{B_1}=\widehat{B_2}\) ( cmt )
\(\Rightarrow\text{ }\Delta ABD=\Delta AED\text{ }\left(ch-gn\right)\)
\(\Rightarrow\text{ }AD=DE\text{ }\left(2\text{ cạnh tương ứng }\right)\)
\(\Rightarrow\text{ }\Delta DAE\text{ cân }\)
c, Trong \(\Delta DEC\text{ }\) vuông tại E có : DC là cạnh đối diện với \(\widehat{E}\) nên \(DC\) là cạnh có độ dài lớn nhất \(\Rightarrow\text{ }DE< DC\)
Mà \(DA=DE\text{ nên }DA< DC\)
d, Vì \(\hept{\begin{cases}DE\text{ }\perp\text{ }BC\\BF\text{ }\perp\text{ }CF\\AB\text{ }\perp\text{ }AC\end{cases}}\text{ }\Rightarrow\text{ }DE\text{ , }AB\text{ và }BF\text{ là đường cao của }\Delta OBC\)
\(\Rightarrow\text{ }AB\text{, }DE\text{ và }CF\text{ đồng quy tại 1 điểm}\)

a: Xét ΔCBA có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{30}=\dfrac{CD}{40}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=50
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{50}{7}\)
=>\(BD=\dfrac{150}{7}\left(cm\right);CD=\dfrac{200}{7}\left(cm\right)\)
Xét ΔABC có DE//AB
nên \(\dfrac{DE}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{DE}{30}=\dfrac{200}{7}:50=\dfrac{4}{7}\)
=>\(DE=\dfrac{120}{7}\left(cm\right)\)
b: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
=>Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot30\cdot40=15\cdot40=600\left(cm^2\right)\)

a)BD là tia phân giác =>AD/DC=AB/BC(tính chất đường phân giác)
CE là tia phân giác=>AE/EB=AC/BC(tính chất dg pg
mà AB=AC nên=> AD/DC=AE/EB=>ED//BC.
b)BD là tia phân giác =>AD/DC=AB/AC=>AD/AB=DC/CB=(AD+DC)/(BC+AB)=b/a+b=>AD=b^2/a+b.
DE//BC=>AD/AC=DE/BC=>DE=AD/AC*BC=b/(a+b)*a=ab/(a+b)
=>1/DE=(a+b)/ab=1/a+1/b