Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(AM=\dfrac{1}{2}AB\)
=>\(S_{AMC}=\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{2}\cdot27=13,5\left(cm^2\right)\)
Vì \(AN=\dfrac{1}{3}AC\)
nên \(S_{AMN}=\dfrac{1}{3}\cdot S_{AMC}=\dfrac{1}{3}\cdot13,5=4,5\left(cm^2\right)\)

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

SABN = \(\dfrac{1}{4}\) SABC ⇒ SABN = 240 : 4 = 60 (cm2)
SAMN = \(\dfrac{1}{4}\) SABN ⇒ SAMN = 60 : 4 = 15 (cm2)
Do SABN = SACM = \(\dfrac{1}{4}\) SABC ⇒ SBIM = SCIN

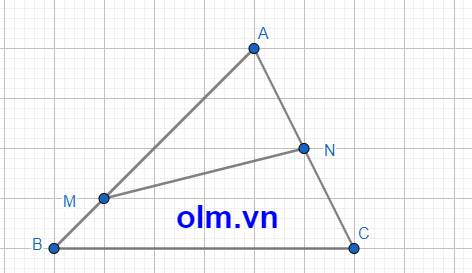
SAMN = \(\dfrac{1}{2}\) SAMC (vì hai tam giác có chung đường cao hạ từ đỉnh M xuống đáy AC và AN = \(\dfrac{1}{2}\)AC)
SAMC = \(\dfrac{3}{4}\) SABC (vì hai tam giác có chung đường cao hạ từ đỉnh C xuống đáy AB và (AM = \(\dfrac{3}{4}\) AB)
⇒SAMN = SABC \(\times\) \(\dfrac{3}{4}\) \(\times\) \(\dfrac{1}{2}\) = \(\dfrac{3}{8}\) \(\times\) SABC
SABC = 48 : \(\dfrac{3}{8}\) = 128 (cm2)
Kết luận diện tích tam giác ABC là 128 cm2

Diện tích tam giác MNB là:
36:3x2=24(cm2)
Diện tích tam giác ABN hay diện tích tam giác BNC là:
36+24=60(cm2)
Diện tích tứ giác BMNC là:
24+60=84(cm2)
Đáp số: 84 cm2
SAMN= 90 x 1/3 x 1/3 = 10 ( cm2)