Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Cách 1: Số phức z được biểu diễn bởi điểm M(x;y).
Số phức z 1 được biểu diễn bởi điểm A(1;-1).
Em có: z − 1 + i = 2 ⇒ MA = 2 .
Vậy tập hợp điểm M là đường tròn tâm A(1;-1), bán kính R = 2 và có phương trình: x − 1 2 + y + 1 2 = 4 .
Cách 2: Đặt z = x + yi , x ; y ∈ ℝ . Số phức z được biểu diễn bởi điểm M(x;y).
Em có:
z − 1 + i = 2 ⇔ x − 1 + y + 1 i = 2 ⇔ x − 1 2 + y + 1 2 = 2 ⇔ x − 1 2 + y + 1 2 = 4
Vậy tập hợp điểm M là đường tròn tâm I(1;-1), bán kính R = 2 và có phương trình:
x − 1 2 + y + 1 2 = 4 .

Đáp án A.
Cách 1: w = 1 + i 3 z + 2 ⇔ z = w − 2 1 + i 3 . Từ đó
z − 1 ≤ 2 ⇔ w − 2 1 + i 3 − 1 ≤ 2 ⇔ w − 3 − i 3 ≤ 2 1 + i 3 ⇔ w − 3 + i 3 ≤ 4
Vậy tập hợp cần tìm là hình tròn tâm I 3 ; 3 bán kính R = 4 . Chọn đáp án A.
Cách 2: Gọi w = x + y i ; x , y ∈ ℝ . Khi đó ta có
w = 1 + i 3 z + 2 ⇔ x + y i = 1 + i 3 z + 2 ⇔ x − 2 + y i 1 + i 3 = z
⇒ z − 1 = x − 2 + y i 1 + i 3 − 1 = x − 3 − y − 3 i 1 + i 3 ⇒ z − 1 = x − y 3 + i y − x 3 + 4 3 4
z − 1 ≤ 2 ⇒ x − y 3 2 + y − x 3 + 4 3 2 ≤ 8 ⇒ x − 3 2 + y − 3 2 ≤ 16 .
Vậy tập hợp cần tìm là hình tròn tâm I 3 ; 3 bán kính R = 4 . Chọn đáp án A.
Bài toán tổng quát: Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số w = α z + β trong đó z là số phức tùy ý thỏa mãn z − z 0 ≤ R ( z 0 , α ≠ 0 , β là những số phức cho trước, R là số thực dương cho trước).
Tương tự như lời giải trên, ta có tập hợp cần tìm là hình tròn có tâm là điểm biểu diễn số phức α z 0 + β , với bán kính bằng R α .

Đáp án A.
Cách 1: w = 1 + i 3 z + 2 ⇔ z = w - 2 1 + i 3 . Từ đó
z - 1 ≤ 2 ⇔ w - 2 1 + i 3 - 1 ≤ 2 ⇔ w - 3 - i 3 ≤ 2 1 + i 3 ⇔ w - 3 + i 3 ≤ 4 .
Vậy tập hợp cần tìm là hình tròn tâm I( 3 ; 3 ) bán kính R = 4. Chọn đáp án A.
Cách 2: Gọi w = x + y i ; x , y ∈ ℝ . Khi đó ta có
w = 1 + i 3 z + 2 ⇔ x + y i = 1 + i 3 z + 2 ⇔ x - 2 + y i 1 + i 3 = z
⇒ z - 1 = x - 2 + y i 1 + i 3 - 1 = x - 3 - y - 3 i 1 + i 3 ⇒ z - 1 = x - y 3 + i y - x 3 + 4 3 4
z - 1 ≤ 2 ⇒ x - y 3 2 + y - x 3 + 4 3 2 ≤ 8 ⇒ x - 3 2 + y - 3 2 ≤ 16 .
Vậy tập hợp cần tìm là hình tròn tâm I( 3 ; 3 ) bán kính R = 4. Chọn đáp án A.
Bài toán tổng quát: Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số w = α z + β trong đó z là số phức tùy ý thỏa mãn z - z 0 ≤ R ( z 0 , α ≢ 0 , β là những số phức cho trước, R là số thực dương cho trước).
Tương tự như lời giải trên, ta có tập hợp cần tìm là hình tròn có tâm là điểm biểu diễn số phức α z 0 + β , với bán kính bằng R α .

Chọn đáp án A.

(Chi tiết tìm đọc trong sách “Công phá kĩ thuật Casio” do Lovebook phát hành.)
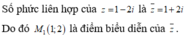

Đáp án A.
Số phức liên hợp của z = 1 − 2 i là z ¯ = 1 + 2 i .
Do đó M 1 1 ; 2 là điểm biểu diễn của z ¯ .