Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) mx2 – 2x – 4m – 1 = 0 (1)
Với m ≠ 0, ta có:
Δ’ = 1 + m.(4m + 1) = 4m2 + m + 1
= 
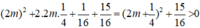với mọi m.
Hay phương trình (1) có hai nghiệm phân biệt với mọi m ≠ 0.
b) x = -1 là nghiệm của phương trình (1)
⇔ m.(-1)2 – 2.(-1) – 4m – 1 = 0
⇔ m + 2 - 4m = 0
⇔ -3m + 1 = 0
⇔ m = 1/3.
Vậy với m = 1/3 thì phương trình (1) nhận -1 là nghiệm.
Khi đó theo định lý Vi-et ta có: x2 + (-1) = 2/m (x2 là nghiệm còn lại của (1))
⇒ x2 = 2/m + 1= 6 + 1 = 7.
Vậy nghiệm còn lại của (1) là 7.
a: Ta có: \(\left(m-1\right)x^2-2x-m+1=0\)
a=m-1; b=-2; c=-m+1
\(ac=\left(m-1\right)\left(-m+1\right)=-\left(m-1\right)^2< 0\forall m\)
Do đó: Phương trình luôn có hai nghiệm trái dấu
b: \(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(\dfrac{2}{m-1}\right)^2-2\cdot\dfrac{-m+1}{m-1}=6\)
\(\Leftrightarrow\dfrac{4}{\left(m-1\right)^2}=4\)
\(\Leftrightarrow\left(m-1\right)^2=1\)
=>m-1=1 hoặc m-1=-1
=>m=2 hoặc m=0
b) Theo hệ thức Vi ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{2m-2}{m}\\x_1.x_2=\dfrac{m-1}{m}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=\dfrac{2-2m}{m}\\x_1.x_2=\dfrac{m-1}{m}\end{matrix}\right.\)
Ta có:
\(Q=\dfrac{1013}{x_1}+\dfrac{1013}{x_2}+1=1013\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)+1\)
\(=1013\left(\dfrac{x_1+x_2}{x_1.x_2}\right)+1=1013\left(\dfrac{\dfrac{2-2m}{m}}{\dfrac{m-1}{m}}\right)+1\)
\(=1013.\dfrac{-2\left(m-1\right)}{m-1}+1=-2026+1=-2025\), luôn là hằng số (đpcm)
a: Δ=(2m-1)^2-4(m-1)
=4m^2-4m+1-4m+4
=4m^2-8m+5
=4m^2-8m+4+1=(2m-2)^2+1>=1>0 với mọi m
=>PT luôn có 2 nghiệm với mọi m
b: x1^3+x2^3=2m^2-m
=>(x1+x2)^3-3x1x2(x1+x2)=2m^2-m
=>(2m-1)^3-3(m-1)(2m-1)=2m^2-m
=>8m^3-12m^2+6m-1-3(2m^2-3m+1)-2m^2+m=0
=>8m^3-14m^2+7m-1-6m^2+9m-3=0
=>8m^3-20m^2+16m-4=0
=>m=1/2 hoặc m=1
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>m2-4>0
=>m>2 hoặc m<-2
Phương trình đã cho nghiệm đúng với hay phương trình có vô số nghiệm khi
m 2 − 3 m + 2 = 0 − ( m 2 + 4 m + 5 ) = 0 ⇔ m = 1 m = 2 m ∈ ∅ ⇔ m ∈ ∅
Đáp án cần chọn là: D
Gọi x 0 là một nghiệm của phương trình x 2 - m x + 2 = 0
Suy ra 3 – x0 là một nghiệm của phương trình x 2 + 2 x - m = 0 .
Khi đó, ta có hệ
x 0 2 − m x 0 + 2 = 0 ( 3 − x 0 ) 2 + 2 ( 3 − x 0 ) − m = 0 ⇔ x 0 2 − m x 0 + 2 = 0 ( 1 ) m = x 0 2 − 8 x 0 + 15 ( 2 )
Thay (2) vào (1), ta được: x 0 2 − ( x 0 2 − 8 x 0 + 15 ) x 0 + 2 = 0 ⇔ x 0 = 2 x 0 = 7 ± 3 5 2 cho ta 3 giá trị của m cần tìm.
Đáp án cần chọn là: D